Exercícios sobre o gráfico da função do segundo grau
O gráfico a seguir pertence a uma função f(x) do segundo grau, com domínio e contradomínio no conjunto dos números reais. A respeito dessas funções, assinale a alternativa correta:
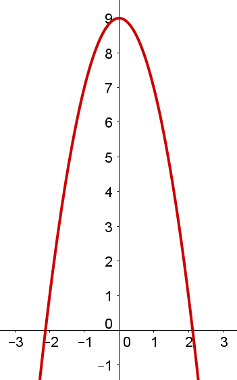
a) Toda função do segundo grau pode ser escrita na forma ax2 + bx + c = 0.
b) O coeficiente “a” dessa função é positivo.
c) O valor do coeficiente “c”, nessa função, é igual a 9.
d) Não é possível determinar as raízes dessa função unicamente a partir de seu gráfico. Para isso, a lei de formação sempre será necessária.
e) f(2) = 0 e f(-2) = 0
a) Incorreta!
A forma apresentada na alternativa é referente às equações do segundo grau. Para haver função, são necessárias duas variáveis. Nesse caso, existe apenas a incógnita x.
b) Incorreta!
O coeficiente “a” de uma função do segundo grau indica a concavidade da parábola. Nesse caso, a concavidade está voltada para baixo e isso acontece sempre que a < 0. Se a > 0, então a concavidade é voltada para cima.
c) Correta!
O coeficiente “c” sempre determina o ponto de encontro da função com o eixo x do plano cartesiano.
d) Incorreta!
As raízes de uma função são os pontos de encontro entre o gráfico dessa função e o eixo x. nesse caso, são números próximos de 2 e – 2.
e) Incorreta!
Na função, f(2) = 0 indicaria que o ponto (2, 0) pertence à função, o que não é verdade. O mesmo vale para a função avaliada em f(– 2)
Gabarito: Alternativa C.
A função f(x) = 2x2 + 4x – 6 está definida nos números reais. A respeito do gráfico dessa função, assinale a alternativa que for correta:
a) O vértice dessa função possui as coordenadas (1, – 8).
b) Uma das raízes dessa função possui as coordenadas (1, 0).
c) A concavidade dessa função está voltada para baixo. Isso acontece porque o valor do coeficiente a é negativo.
d) O coeficiente “c” dessa função é exatamente – 8, pois c é referente ao ponto mais baixo de uma função com concavidade voltada para cima.
e) O coeficiente “c” dessa função é exatamente 8, pois c é referente ao ponto mais alto de uma função com concavidade voltada para baixo.
a) Incorreta!
Para determinar o vértice de uma função, sem conhecer seu gráfico, existem algumas técnicas. A mais conhecida delas é o uso das fórmulas:
xv = – b
2a
e
yv = – ∆
4a
Calculando xv, teremos:
xv = – b
2a
xv = – 4
2·2
xv = – 4
4
xv = – 1
Como a coordenada x dada pela alternativa é 1, então não é necessário procurar yv. A alternativa está errada.
b) Correta!
As coordenadas dadas são x = 1 e y = 0. Fazendo x = 1 na função, teremos:
f(x) = 2x2 + 4x – 6
y = 2·12 + 4·1 – 6
y = 2 + 4 – 6
y = 6 – 6
y = 0
Logo, verifica-se que, se x = 1, y = 0.
c) Incorreta!
O coeficiente a, quando positivo, indica que a concavidade da parábola está voltada para cima.
d) Incorreta!
O coeficiente c indica o ponto de encontro de uma parábola com o eixo y. No geral, ele não indica o ponto mais alto ou mais baixo de uma função. A indicação desse ponto é feita pelo vértice.
e) Incorreta!
O coeficiente c indica o ponto de encontro de uma parábola com o eixo y. No geral, ele não indica o ponto mais alto ou mais baixo de uma função. A indicação desse ponto é feita pelo vértice.
Gabarito: Alternativa B.
A função f(x) = x2 + 6x – 36, definida nos números reais, possui ponto de mínimo de coordenadas:
a) (3, 45)
b) (3, – 45)
c) (– 3, 45)
d) (0,0)
e) (– 3, – 45)
Sempre que uma função possui concavidade voltada para cima, ela possui ponto de mínimo localizado no vértice. Sendo assim, basta calcular as coordenadas do vértice para determinar o ponto de mínimo de uma função do segundo grau (que possui concavidade voltada para cima).
Para tanto, podemos usar as seguintes fórmulas para encontrar x do vértice e y do vértice:
xv = – b
2a
xv = – 6
2·1
xv = – 6
2
xv = – 3
yv = – ∆
4a
yv = – (62 – 4·1·[–36])
4·1
yv = – (36 – 4·[–36])
4
yv = – (36 + 144)
4
yv = – (180)
4
yv = – 45
As coordenadas do ponto de mínimo são: (– 3, – 45)
Gabarito: Alternativa E.
Quais os pontos de encontro do gráfico da função f(x) = x2 + 6x + 8, definida nos números reais, com o eixo x do plano cartesiano?
a) (2, 0) e (4, 0)
b) (– 2, 0) e (4, 0)
c) (2, 0) e (– 4, 0)
d) (– 2, 0) e (– 4, 0)
e) (0, – 2) e (0, – 4)
Os pontos de encontro do gráfico de uma função com o eixo x do plano cartesiano são as raízes de uma função. Para calculá-las, podemos usar a fórmula de Bháskara ou qualquer outra técnica conhecida. Para esse exercício, usaremos a técnica de completar quadrados usando produtos notáveis. Lembrando que as raízes de uma função são encontradas fazendo f(x) = 0.
f(x) = x2 + 6x + 8
0 = x2 + 6x + 8
x2 + 6x + 8 = 0
x2 + 6x + 8 + 9 = 9
x2 + 6x + 9 = 9 – 8
(x + 3)2 = 1
√[(x + 3)2] = √1
x + 3 = ± 1
x = ± 1 – 3
x’ = 1 – 3 = – 2
x’’ = – 1 – 3 = – 4
Os pontos de encontro da função com o eixo x são: (– 2, 0) e (– 4, 0).
Gabarito: Alternativa D.
