Exercícios sobre Inequações polinomiais do 1º grau
Um engenheiro, ao realizar seus cálculos para o seu projeto de construção, obtém uma desigualdade. Então ele precisa obter qual intervalo que satisfaz essa desigualdade para completar o seu projeto, ajude-o a obter esta solução. A inequação obtida é: 4x -20 > 12.
Basta isolarmos o x na desigualdade para acharmos a condição de x desta inequação.
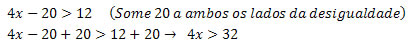
Como 4 é maior que zero, podemos dividir os dois lados da desigualdade por 4 sem mudar seu sentido.
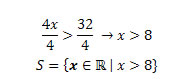
Lembre-se: Em qualquer inequação, antes de multiplicar ou dividir por um número ou expressão algébrica, verifique se este termo é positivo ou negativo, pois quando for negativo, haverá a necessidade de mudança de sentido da desigualdade.
Uma loja compra um pacote de mercadorias do distribuidor pelo valor de R$300,00 e nos é informado que o gerente de vendas pretende vender cada unidade por R$5,00. Com isso podemos afirmar que o lucro final desta empresa será dado em função das x unidades vendidas. Com isso, responda:
a. Qual a lei de formação desta função?
b. Qual será o intervalo dos valores de x em que teremos f(x)<0 ? Analisando no contexto da questão, como este fato pode ser interpretado?
a) Antes de escrevermos em linguagem matemática é necessário compreender o que se passa no problema. Temos que informar qual é a lei de formação da função do lucro. Podemos falar que o lucro é dado da seguinte forma:
LUCRO = Renda das Vendas – Custo de compra da mercadoria
Do lado direito da igualdade temos dois fatores determinantes para a construção da função lucro. A Renda das Vendas depende da quantidade de unidades vendidas, denominaremos essa quantidade de mercadoria pela variável x e o custo de compra da mercadoria que é fixo.
b)
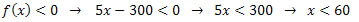
Sabemos que f(x) é a função do lucro, ao fazermos f(x) < 0 estamos encontrando um intervalo onde o lucro será negativo; em outras palavras, determinamos a quantidade de unidades vendidas que acarretarão prejuízo para a empresa, ou seja, caso a empresa venda menos de 60 unidades no mês ela fechará o mês com saldo negativo.
(EEM-SP)
Uma empresa produz trufas de chocolate, cujo custo de fabricação pode ser dividido em duas partes: uma independente da quantidade vendida, de R$ 1500,00 mensais; outra depende da quantidade fabricada, de R$ 0,50 por unidade.
Escreva a(as) expressão(ões) que permita(m) determinar o número de trufas que devem ser vendidas num mês para que a empresa não tenha prejuízo, sabendo-se que o preço de venda de cada unidade é de R$ 1,50.
Esta questão é bem similar à anterior, com uma diferença apenas. O custo da empresa agora depende de dois fatores, um deles é fixo (R$1500,00) e o outro depende da quantidade de unidades produzidas.
.jpg)
Para que não tenha prejuízo, o lucro tem que ser maior ou igual a zero. Façamos a inequação:
.jpg)
Ou seja, a quantidade de unidades de trufas a serem vendidas tem que ser maior ou igual a 1500, caso contrário, a empresa terá prejuízos.
O dono de uma fábrica de calçados solicitou os serviços de um administrador para que este o auxilie nas contas de sua fábrica, para que esta não dê prejuízo. Para isso o administrador pediu ao dono desta fábrica três informações: custo operacional mensal, custo de cada mercadoria produzida, quantidade média de unidades vendidas ao mês.
Custo operacional mensal: R$ 2000,00
Custo de cada mercadoria: R$ 2,00
Quantidade média de vendas mensal: 502 unidades
Com isso, qual deve ser o valor de cada mercadoria de forma que a fábrica não leve prejuízo?
O lucro da empresa dependerá do valor da mercadoria, pois o dono da fábrica tem uma quantidade “fixa” de vendas por mês, logo teremos a seguinte função:
Assim, para que esta empresa não tenha prejuízo, deverá vender seus calçados a um preço maior ou igual a R$ 4,00.
(PUC-SP)
O menor número inteiro k que satisfaz a inequação 8 - 3 (2k-1) < 0.
Para encontrarmos qual número é este é necessário resolver primeiramente a desigualdade, pois assim obteremos uma condição para o valor k.
.jpg)
O próximo número inteiro maior que 1,8333... é o número 2, sendo este o menor número inteiro que satisfaz a desigualdade.
