Exercícios sobre lei dos cossenos
(UF- Viçosa) Dois lados de um terreno de forma triangular medem 15 m e 10 m, formando um ângulo de 60°, conforme a figura abaixo:
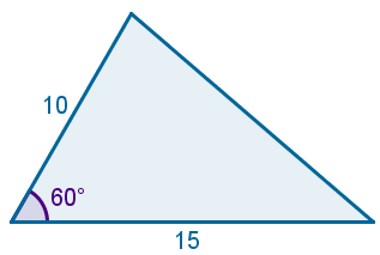
O comprimento do muro necessário para cercar o terreno, em metros, é:
a) 5(5 + √15)
b) 5(5 + √5)
c) 5(5 + √13)
d) 5(5 + √11)
e) 5(5 + √7)
O comprimento do muro necessário para cercar o terreno é igual ao seu perímetro. Para esse cálculo, basta somar os comprimentos do lado do triângulo.
10 + 15 + x
O valor de x pode ser encontrado por meio da lei dos cossenos:
x2 = 102 + 152 – 2·10·15·cos60°
x2 = 100 + 225 – 2·150·cos60°
x2 = 325 – 300·1/2
x2 = 325 – 150
x2 = 175
x = √175
x = √[5·35]
x = √[5·5·7]
x = √[52·7]
x = 5√7
Logo, a soma que representa o perímetro desse triângulo é:
10 + 15 + x
25 + 5√7
5·5 + 5√7
5(5 + √7)
Gabarito: Letra E.
(UF- Juiz de Fora) Dois lados de um triângulo medem 8 m e 10 m e formam um ângulo de 60°. O terceiro lado desse triângulo mede:
a) 2√21 m
b) 2√31 m
c) 2√41 m
d) 2√51 m
e) 2√61 m
Geralmente, o melhor caminho para resolver exercícios que apresentam dois lados e um ângulo entre eles de um triângulo é a lei dos cossenos. O lado oposto ao ângulo será x e todos esses lados serão colocados na fórmula seguinte:
x2 = a2 + b2 – 2·a·b·cosα
*a e b são os lados que formam o ângulo α. Substituindo os valores nessa fórmula, teremos:
x2 = 82 + 102 – 2·8·10·cos60
x2 = 64 + 100 – 2·80·1/2
x2 = 164 – 2·40
x2 = 164 – 80
x2 = 84
x = √84
x = √[2·2·21]
x = 2√21
O terceiro lado desse triângulo mede 2√21. Gabarito: Letra A.
Calcule a medida do lado x do triângulo abaixo sabendo que o ângulo oposto a ele mede 60°.
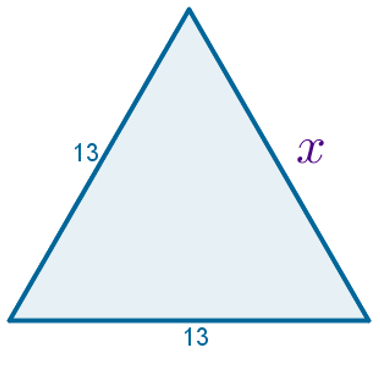
a) 9
b) 10
c) 11
d) 12
e) 13
A partir da lei dos cossenos, dada pela fórmula abaixo, teremos:
x2 = a2 + b2 – 2·a·b·cosα
Sabendo que o ângulo oposto a x mede 60° e que as medidas de a e b são 13, teremos:
x2 = 132 + 132 – 2·13·13·cos60
x2 = 169 + 169 – 2·13·13·cos60
x2 = 169 + 169 – 2·169·1/2
Colocando 169 em evidência:
x2 = 169(1 + 1 – 2·1/2)
x2 = 169(1 + 1 – 1)
x2 = 169(1)
x2 = 169
x = √169
x = 13
Outra forma de resolver esse problema: sabendo que um triângulo equilátero possui todos os lados e ângulos iguais e que seus ângulos são iguais a 60°, é possível mostrar pelo caso LAL que o triângulo do exercício é congruente a um triângulo equilátero de lado 13. Logo, o último lado também mede 13.
Gabarito: Letra E.
Qual é a medida do lado oposto ao ângulo de 30°, em um triângulo, sabendo que os outros dois lados medem 2 e √3?
a) 1
b) 1,5
c) 2
d) 2,5
e) 3
Seja o lado oposto ao ângulo de 30° igual a x, podemos usar a lei dos cossenos para descobrir seu valor. Para tanto:
x2 = a2 + b2 – 2·a·b·cosα
x2 = 22 + (√3)2 – 2·2·√3·cos30
x2 = 4 + 3 – 2·2·√3·√3/2
x2 = 7 – 4·3/2
x2 = 7 – 12/2
x2 = 7 – 6
x2 = 1
x = 1
O lado oposto ao ângulo de 30° mede 1. Gabarito: Letra A.
