Exercícios sobre matriz triangular
Analise a matriz M a seguir:
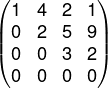
Podemos afirmar que a matriz M é:
A) uma matriz identidade.
B) uma matriz triangular superior.
C) uma matriz triangular inferior.
D) uma matriz transposta.
E) uma matriz inversível.
Alternativa B. Note que a matriz possui elementos não nulos acima da diagonal principal e que, abaixo da diagonal principal, todos os seus elementos são iguais a zero, o que faz com que essa matriz seja uma matriz triangular superior.
O determinante da matriz a seguir é igual a:
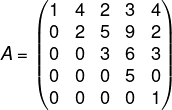
A) 0.
B) 6.
C) 9.
D) 25.
E) 30.
Alternativa E. Como A é uma matriz triangular, o determinante dessa matriz é igual à multiplicação dos termos da diagonal principal.
det (A) = 1 · 2 · 3 · 5 · 1 = 30
Uma matriz M3x3 é construída pelos elementos mij tal que:
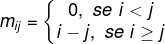
Ao construir a matriz M, podemos afirmar que:
A) M é uma matriz triangular inferior.
B) M é uma matriz triangular superior.
C) M é uma matriz identidade.
D) M é uma matriz quadrada não triangular.
E) M é uma matriz nula.
Alternativa A. A matriz é de ordem 3, então vamos encontrar cada um dos seus termos, levando em consideração a condição citada na questão, ou seja, quando o número de linhas é menor que o número de colunas, o termo é igual a zero; caso o número de linhas seja maior ou igual ao número de colunas, o termo é a diferença entre a linha e a coluna.
m11 = 1 – 1 = 0
m12 = 0
m13 = 0
m21 = 2 – 1 = 1
m22 = 2 – 2 = 0
m23 = 0
m31= 3 – 1 = 2
m32= 3 – 2 = 1
m33= 3 – 3 = 0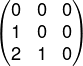
A matriz é triangular inferior.
Dadas as matrizes A e B, para qual valor de x o produto A · B é igual a uma matriz triangular?
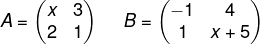
A) – 7/5.
B) – ¾.
C) + 4/3.
D) – 5/7.
E) – 1.
Alternativa D.
Multiplicando as matrizes, temos que:
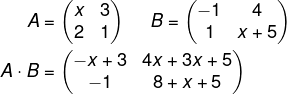
Para que a matriz seja triangular, faremos:
4x + 3x + 5 = 0
7x + 5 = 0
7x = – 5
x = – 5/7
Julgue as afirmativas a seguir sobre matriz triangular.
I. Toda matriz triangular é uma matriz quadrada.
II. O determinante da matriz triangular é igual ao produto da diagonal principal.
III. A soma de uma matriz triangular superior e uma matriz triangular inferior é também uma matriz triangular.
Marque a alternativa correta.
A) Apenas I e II são falsas.
B) Apenas II e III são falsas.
C) Apenas a III é falsa.
D) Apenas a II é falsa.
E) Todas são verdadeiras.
Alternativa C.
I → Verdadeira, pois toda matriz triangular é quadrada.
II → Verdadeira, pois uma das propriedades da matriz triangular é que seu determinante é o produto dos termos da diagonal principal.
III → Falsa. Ao realizar a soma de uma matriz triangular inferior e uma matriz triangular superior, a resposta é uma matriz que não é triangular.
A soma da matriz M com a matriz N é uma matriz triangular inferior; sendo assim, o valor da expressão numérica a – b + c é igual a:
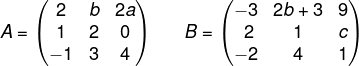
A) – 5,5.
B) – 3,5.
C) 1.
D) 3,0.
E) 5.
Alternativa B.
Para que a soma A + B seja triangular superior, temos que:
I) b + 2b + 3 = 0
Resolvendo a equação:
3b + 3 = 0
3b = – 3
b = – 3/3
b = – 1
II) 2a + 9 = 0
Resolvendo a equação:
2a + 9 = 0
a = – 9/2
a = – 4,5
c = 0
Agora vamos calcular a expressão:
a – b + c
– 4,5 – ( – 1) + 0
– 4,5 + 1
– 3,5
Seja B uma matriz de ordem 2 e triangular superior, então a matriz transposta de B:
A) é uma matriz triangular superior.
B) é uma matriz triangular inferior.
C) não é uma matriz triangular.
D) é uma matriz identidade.
Alternativa B.
Como B é uma matriz triangular, então:
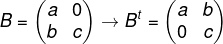
Note que Bt é uma matriz triangular inferior.
Analise as matrizes A, B e C.
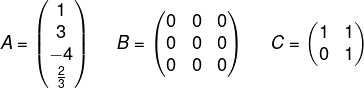
As matrizes A, B e C são casos especiais de matrizes, sendo conhecidas, respectivamente, como:
A) matriz linha, matriz nula e matriz identidade.
B) matriz linha, matriz identidade e matriz triangular.
C) matriz coluna, matriz nula e matriz identidade.
D) matriz coluna, matriz nula e matriz triangular.
E) matriz coluna, matriz triangular e matriz identidade.
Alternativa D.
A → É uma matriz coluna, pois possui só uma coluna.
B → É uma matriz nula, pois todos os seus termos são iguais a zero.
C → É uma matriz triangular superior, pois os termos abaixo da diagonal principal são iguais a zero.
As matrizes podem ser classificadas de acordo com as suas características. Analise as alternativas a seguir e marque a que contém uma matriz triangular inferior.
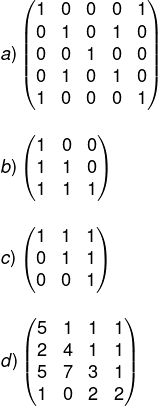
Alternativa B.
A matriz que contém os termos acima da diagonal principal iguais a zero é conhecida como matriz triangular inferior. A única alternativa que satisfaz a definição é a B.
Sobre as propriedades de uma matriz triangular, podemos afirmar que:
I → o determinante é a soma dos elementos da diagonal principal.
II → se um dos termos da diagonal principal for zero, então a matriz triangular não será inversível.
III → a soma de duas matrizes triangulares superiores é uma matriz triangular superior.
Estão corretas:
A) somente I e II.
B) somente II e III.
C) somente I e III.
D) todas as afirmativas.
E) nenhuma das afirmativas.
Alternativa B.
I → Falsa, pois é o produto dos termos da diagonal principal, e não a soma.
II → Verdadeira, pois a matriz é inversível quando o determinante é diferente de zero. Se há um termo igual a zero na diagonal principal, então o determinante da matriz triangular é zero, o que faz com que ela não seja inversível.
III → Verdadeira. Como os termos abaixo da diagonal principal são iguais a zero em ambas, então eles continuarão sendo zero na soma.
Considere a matriz a seguir.
O seu determinante é igual a:
A) 9.
B) 15.
C) 12.
D) 0.
E) 45.
Alternativa E.
Essa matriz é triangular inferior, e o determinante de uma matriz triangular é o produto da diagonal principal, independentemente da ordem da matriz. Então, temos que:
det(A) = 1·3·3·1·5 = 45
(FAU) Dada uma matriz A triangular superior e uma matriz B diagonal, a multiplicação dessas matrizes, ou seja, AB, resultará em uma matriz do tipo?
A) Identidade.
B) Triangular inferior.
C) Diagonal.
D) Triangular superior.
E) Nula.
Alternativa D.
Como a questão não informa a ordem da matriz, faremos a partir da mais simples. Suponha que ela seja uma matriz de ordem 2, então:
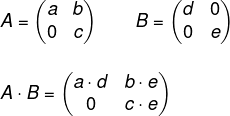
AB é uma matriz triangular superior.
