Exercícios sobre média ponderada
A média ponderada dos números 5, 12, 20 e 15 com pesos respectivamente iguais a 1, 2, 3 e 4 é:
A) 16,0
B) 14,9
C) 17,2
D) 17,8
E) 18,0
Alternativa B
Calculando a média:
\(x=\frac{5\cdot1+12\cdot2+20\cdot3+15\cdot4}{1+2+3+4}\)
\(x=\frac{5+24+60+60}{10}\)
\(x=\frac{149}{10}\)
\(x=14,9\ \)
A média ponderada entre os números 2, x e 5, com pesos respectivamente iguais a 10, 12 e 13, é igual a 3,8. Então, o valor de x é:
A) 3
B) 4
C) 5
D) 6
E) 7
Alternativa B
Sabemos que:
\(3,8=\frac{2\cdot10+12x+5\cdot13}{10+12+13}\)
\(3,8=\frac{20+12x+65}{35}\)
\(3,8\cdot35=12x+85\)
\(133=12x+85\)
\(133-85=12x\)
\(48=12x\)
\(x=\frac{48}{12}\)
\(x=4\)
A temperatura máxima de uma cidade ao longo de 20 dias foi anotada na lista a seguir:
|
Temperatura |
Frequência |
|
37° |
9 |
|
36° |
4 |
|
35° |
2 |
|
34° |
5 |
Podemos afirmar que a temperatura média dessa cidade nesses 20 dias foi de:
A) 34,65°
B) 35,20°
C) 35,85°
D) 36,00°
E) 36,25
Alternativa C
Calculando a temperatura média:
\(x=\frac{37\cdot9+36\cdot4+35\cdot2+34\cdot5}{20}\)
\(x=\frac{333+144+70+170}{20}\)
\(x=\frac{717}{20}\)
\(x=35,85\)
Na disciplina de Probabilidade de uma universidade federal, o professor estabeleceu que os estudantes fariam 3 provas, P1, P2 e P3, e essas provas teriam, respectivamente, pesos 2, 3 e 5. Considere que a média é 6,0. Se um estudante tirou 4 na primeira prova e 6 na segunda, qual será a nota mínima necessária na terceira prova para que ele seja aprovado?
A) 6,4
B) 6,5
C) 6,8
D) 7,1
E) 7,4
Alternativa C
Para que ele seja aprovado, é necessário que a sua média seja igual a 6. Sendo y a nota da P3:
\(6=\frac{2\cdot4+3\cdot6+y\cdot5}{2+3+5}\)
\(6=\frac{8+18+5y}{10}\)
\(60=26+5y\)
\(60-26=5y\)
\(34=5y\)
\(y=\frac{34}{5}\)
\(y=6,8\)
O salário dos funcionários de determinada empresa consta na tabela abaixo:
|
Cargo |
Salário |
Quantidade |
|
Auxiliar administrativo |
R$ 1800,00 |
2 |
|
Vendedores |
R$ 2500,00 |
26 |
|
Supervisores |
R$ 5000,00 |
8 |
|
Gerente de vendas |
R$ 8000,00 |
4 |
Analisando a tabela, podemos afirmar que a média salarial dessa empresa é:
A) R$ 2460,00
B) R$ 2900,00
C) R$ 3455,00
D) R$ 3515,00
E) R$ 4050,00
Alternativa D
Calculando a média, temos que:
\(x=\frac{2\cdot1800+26\cdot2500+8\cdot5000+4\cdot8000}{2+26+8+4}\)
\(x=\frac{3600+65000+40000+32000}{40}\)
\(x=\frac{140600}{40}\)
\(x=3515\)
A média aritmética entre dois números é 5, e a média ponderada entre esses números, com pesos 2 e 3, é igual a 5,2. Assim, podemos afirmar que o produto entre esses números é:
A) 14
B) 15
C) 18
D) 20
E) 24
Alternativa E
Sendo x e y esses dois números, temos que:
\(\frac{x+y}{2}=5\)
\(x+y=5\cdot2\ \)
\(x+y=10\)
Além disso, com pesos 2 e 3, temos que:
\(\frac{2x+3y}{2+3}=5,2\)
\(2x+3y=5,2\cdot5\)
\(2x+3y=26\)
Dessa forma, temos um sistema com duas equações:
\(x+y=10\)
\(2x+3y=26\)
Isolando o x na primeira:
\(x=10-y\)
Substituindo na segunda:
\(2\left(10-y\right)+3y=26\)
\(20-2y+3y=26\)
\(y=26-20\)
\(y=6\)
Sabendo que y = 6, temos que:
\(x+y=10\)
\(x+6=10\ \)
\(x=10-6\)
\(x=4\ \)
Agora, basta calcular o produto:
\(6\cdot4=24\ \)
Em uma empresa de fast-food, após a refeição, os clientes fazem uma avaliação da loja, com nota de 1 a 5 estrelas. Em determinado dia, foram atendidos exatamente 100 clientes, e as notas obtidas foram:
|
Avaliação |
Total de clientes |
|
1 estrela |
2 |
|
2 estrelas |
15 |
|
3 estrelas |
18 |
|
4 estrelas |
25 |
|
5 estrelas |
40 |
Após o fechamento do expediente, o gerente decidiu calcular a nota média das avaliações naquele dia, que foi de, aproximadamente:
A) 3,7
B) 3,9
C) 4,1
D) 4,3
E) 4,5
Alternativa B
Calculando a média:
\(x=\frac{1\cdot2+2\cdot15+3\cdot18+4\cdot25+5\cdot40}{100}\)
\(x=\frac{2+30+54+100+200}{100}\)
\(x=\frac{386}{100}\)
\(x=3,86\)
Arredondando, temos que:
\(x=3,9\)
Durante a seleção de professores para uma escola, foram avaliados três critérios, sendo eles: currículo, entrevista e aula experimental. Para saber qual é a nota do candidato, é feita a média ponderada das notas em cada um dos critérios, com pesos 1, 2 e 3 para currículo, entrevista e aula experimental, respectivamente. Kárita fez essa seleção e tirou as seguintes notas:
- Currículo: 6
- Entrevista: 8
- Aula experimental: 7
Nessas condições, podemos afirmar que a média da Kárita foi de:
A) 7,0
B) 7,2
C) 8,1
D) 8,6
E) 9,0
Alternativa B
Calculando a média, temos que:
\(x=\frac{1\cdot6+2\cdot8+3\cdot7}{1+2+3}\)
\(x=\frac{6+16+21}{6}\)
\(x=\frac{43}{6}\)
\(x=7,166..\)
\(x = {7,2}\)
(Enem 2014) Ao final de uma competição de ciências em uma escola, restaram apenas três candidatos. De acordo com as regras, o vencedor será o candidato que obtiver a maior média ponderada entre as notas das provas finais nas disciplinas Química e Física, considerando, respectivamente, os pesos 4 e 6 para elas. As notas são sempre números inteiros. Por questões médicas, o candidato II ainda não fez a prova final de Química. No dia em que sua avaliação for aplicada, as notas dos outros dois candidatos, em ambas as disciplinas, já terão sido divulgados.
O quadro apresenta as notas obtidas pelos finalistas nas provas finais.
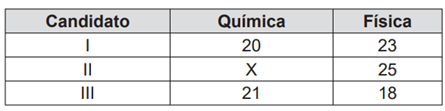
A menor nota que o candidato II deverá obter na prova final de Química para vencer a competição é
A) 18.
B) 19.
C) 22.
D) 25.
E) 26.
Alternativa A
Primeiramente, calcularemos a média dos candidatos I e III, começando pelo candidato I:
\(x_I=\frac{20\cdot4+23\cdot6}{10}\)
\(x_I=\frac{80+138}{10}=\frac{218}{10}=21,8\)
Agora, o candidato III:
\(x_{III}=\frac{21\cdot4+18\cdot6}{10}\)
\(x_{III}=\frac{84+108}{10}=\frac{192}{10}=19,2\)
Então, queremos que a nota do candidato II seja a maior de todas, ou seja, maior que 21,8.
\(\frac{4x+25\cdot6}{10}>21,8\)
\(4x+150>21,8\cdot10\)
\(4x+150>218\)
\(4x>218-150\)
\(4x>68\)
\(x>\frac{68}{4}\)
\(x>17\)
Assim, a nota deve ser no mínimo 18.
(Enem 2019) Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o número obtido em cada jogada, construiu-se a seguinte tabela de distribuição de frequência:
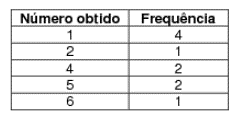
A média, mediana e moda dessa distribuição de frequência são, respectivamente:
A) 3, 2 e 1
B) 3, 3 e 1
C) 3, 4 e 2
D) 5, 4 e 2
E) 6, 2 e 4
Alternativa B
Calculando a média:
\(x=\frac{1\cdot4+2\cdot1+4\cdot2+5\cdot2+6\cdot1}{10}\)
\(x=\frac{4+2+8+10+6}{10}\)
\(x=\frac{30}{10}=3\)
A média é 3.
Sobre a mediana, sabemos que 10 : 2 = 5, então a ela será a soma do 5º com o 6º valor da tabela dividida por 2. O 5º valor é 2, e o 6º é 4, então (2 + 4) : 2 = 3.
A moda é o valor que tem maior frequência, logo podemos afirmar que a moda é 1.
Portanto, a média, mediana e moda são 3, 3 e 1
(Enem 2019) Em uma fábrica de refrigerantes, é necessário que se faça periodicamente o controle no processo de engarrafamento para evitar que sejam envasadas garrafas fora da especificação do volume escrito no rótulo.
Diariamente, durante 60 dias, foram anotadas as quantidades de garrafas fora dessas especificações. O resultado está apresentado no quadro.
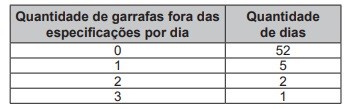
A média diária de garrafas fora das especificações no período considerado é
A) 0,1.
B) 0,2.
C) 1,5.
D) 2,0.
E) 3,0.
Alternativa B
Calculando a média, temos que:
\(x=\frac{0\cdot52+5\cdot1+2\cdot2+1\cdot3}{52+5+2+1}\)
\(x=\frac{0+5+4+3}{60}\)
\(x=\frac{12}{60}\)
\(x = {0,2}\)
(ENEM 2021 — PPL) Uma pessoa realizou uma pesquisa com alguns alunos de uma escola, coletando suas idades, e organizou esses dados no gráfico.
Qual é a média das idades, em ano, desses alunos?
A) 9
B) 12
C) 18
D) 19
E) 27
Alternativa D
Calculando a média ponderada:
\(x=\frac{6\cdot9+12\cdot18+27\cdot9}{6+9+12}\)
\(x=\frac{54+216+243}{27}\)
\(x=\frac{513}{27}\)
\(x=19\)
