Exercícios sobre mínimo múltiplo comum
Estes exercícios testarão seus conhecimentos sobre a resolução de problemas que envolvam a obtenção de mínimo múltiplo comum.
Publicado por: Luiz Paulo Moreira SilvaQuestões
-
Questão 1
Qual é o mínimo múltiplo comum entre os números 90, 150 e 20?
a) 90
b) 150
c) 20
d) 900
e) 450
Para realizar esse cálculo, basta utilizar o método prático:
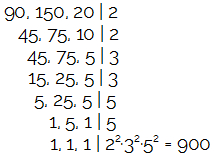
Gabarito: Letra D.
-
Questão 2
Uma loja de aviamentos vende prendedores de cabelo em embalagens com 15 unidades e lacinhos em embalagens com 6 unidades cada uma. Uma pessoa que deseja comprar a mesma quantidade de lacinhos e de prendedores de cabelo deverá comprar quantas embalagens no total?
O MMC entre 15 e 6 dirá exatamente quantas embalagens devem ser compradas no total.
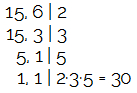
-
Questão 3
(UEM PR/2009 - adaptada)
Considerando os números 60, 110 e 126, assinale o que for correto.
01. 2 é o único divisor positivo par de 110.
02. A soma dos números primos positivos que são simultaneamente divisores de 60 e de 126 é igual a 5.
04. A soma dos divisores positivos do número 110 é igual a 216.
08. O mínimo múltiplo comum entre 60 e 110 é 6600.
16. O máximo divisor comum entre 60 e 126 é 6.
Qual é a soma dos números referentes às alternativas corretas?
a) 22
b) 23
c) 31
d) 11
e) 14
01. Incorreta!
10 também é um divisor par de 110.02. Correta!
2 e 3, cuja soma é 5, são primos positivos que são, simultaneamente, divisores de 60 e 126.04. Correta!
Os divisores do número 110 são: 1, 2, 5, 11, 10, 22, 55 e 110, e a soma entre eles é: 1 + 2 + 5 + 10 + 11 + 22 + 55 + 110 = 21608. Incorreta!
O MMC entre 60 e 110 é:
16. Correta!
O MDC entre 60 e 126 é: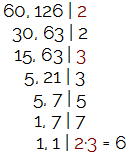
Gabarito: Letra A.
-
Questão 4
(PUC MG/2001)
O Mínimo Múltiplo Comum dos números 23, 3n e 7 é 1512. O valor de n é:
a) 3
b) 4
c) 5
d) 6
O Mínimo Múltiplo Comum também pode ser calculado a partir da decomposição em fatores primos de um número. Para resolver esse exercício, portanto, podemos decompor o número 1512 em fatores primos, sabendo que ele é MMC de 23, 3n e 7, podemos ter certeza de que os fatores primos que aparecerão serão exatamente esses com o expoente do número 3. Observe:
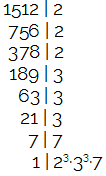
A decomposição em fatores primos é igual ao produto apresentado no texto do exercício. Assim, podemos escrever a igualdade abaixo e concluir que o valor de n é:
23·3n·7 = 23·33·7
n = 3
Gabarito: Letra A.