Exercícios sobre notações de conjuntos
Dados os conjuntos A = {números ímpares entre 1 e 10}, B = {múltiplos de 3 entre 1 e 12}, C = {números pares entre 3 e 11} e D = {múltiplos de 2 entre 1 e 9}, estabeleça as relações existentes entre os conjuntos através do Diagrama de Venn.
Inicialmente identificamos os elementos pertencentes aos conjuntos:
A = {números ímpares entre 1 e 10} → A = {1, 3, 5, 7, 9}
B = {múltiplos de 3 entre 1 e 12} → B = {3, 6, 9, 12}
C = {números pares entre 3 e 11} → C = {4, 6, 8, 10}
D = {múltiplos de 2 entre 1 e 9} → D = {2, 4, 6, 8}
Podemos afirmar que A
B = {3, 9}, AC = Ø, AD = Ø, BC = {6}, BD = {6} e CD = {4, 6, 8}. Vamos agora demonstrar essas relações através do Diagrama de Venn:
.jpg)
Diagrama de Venn que soluciona a questão 1.
Sabendo que AB = {5, 9, 10}, AC = {5}, AD = {2, 9}, BC = {1, 3, 5}, BD = {4, 9}, C.jpg)
D = Ø, A – (BCD) = Ø, B – (ACD) = {12, 15}, C – ( AB) = {8} e D – (AB) = {7}, determine os elementos pertencentes aos conjuntos A, B, C e D.
Para facilitar a visualização dos elementos pertencentes aos conjuntos, vamos montar o Diagrama de Venn a partir das relações apresentadas.
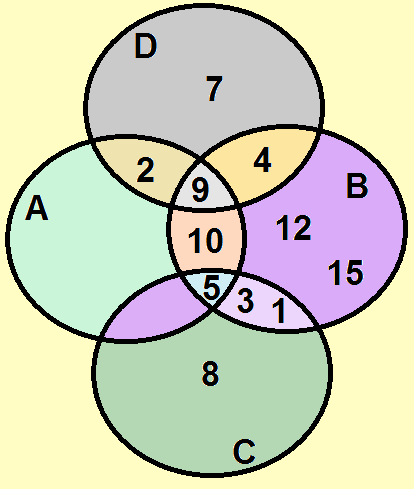
Representação das relações de pertinência dos conjuntos da questão 2
Portanto, podemos afirmar que os conjuntos são: A = {2, 5, 9, 10}, B = {1, 3, 4, 5, 9, 10, 12, 15}, C = {1, 3, 5, 8} e D = {2, 4, 7, 9}.
Sejam os conjuntos A, B e C tais que B
A, B.jpg)
C = ø, AC = {3}, C – A = {1,4}, B – C = {2,6} e A.jpg)
C = {1, 2, 3, 4, 5, 6, 7}. Nessas condições, é verdade que:
a) A – C = {2, 5, 6, 7}
b) BC = {1, 2, 4, 6}
c) AB = {2, 3, 6}
d) C – B = {1, 4
De acordo com o enunciado, podemos afirmar que o conjunto B pertence ao conjunto A, que B e C não possuem elementos em comum, que os conjuntos A e C possuem apenas o elemento 3 em comum, que os elementos 1 e 4 são exclusivos do conjunto C, que 2 e 6 são exclusivos do conjunto B, e que os conjuntos A, B e C possuem juntos os elementos 1, 2, 3, 4, 5, 6 e 7. Para melhor visualizar a distribuição dos elementos nos conjuntos, vejamos a figura a seguir:
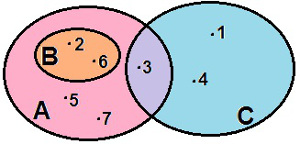
Representação dos conjuntos A, B e C
Para resolver a questão, vamos analisar as alternativas até encontrar a alternativa correta.
a) A – C = {2, 5, 6, 7}. Essa alternativa afirma que, ao olharmos os elementos que pertencem ao conjunto A e que não pertencem ao conjunto C, teremos os elementos {2, 5, 6, 7}. A alternativa está correta, pois basta analisar a figura acima para ver que os elementos {2, 5, 6, 7} estão no conjunto A e não pertencem ao conjunto C.
Como verificamos que a alternativa correta é a letra a, podemos concluir que as demais alternativas estão incorretas.
(Unicruz – RS) Dados: A = {1, 3, 4, 5, 7, 8}, B = {1, 3, 5, 6, 9}, C = {5, 6, 7, 8, 9}, temos que A(BC) resulta:
a) {5, 6, 9}
b) {5}
c) {1, 3}
d) {1, 3, 4, 7, 8}
e) {7, 8}
Primeiramente, vamos identificar os elementos em comum aos conjuntos B e C. Os elementos pertencentes à intercessão desses conjuntos são {5, 6, 9}. Agora precisamos verificar quais desses elementos pertencem também ao conjunto A. O único elemento que obedece a essa definição é o {5}. Portanto, a alternativa correta é a letra b.
