Exercícios sobre operações com conjuntos
Esta lista de exercícios vai te ajudar a testar seus conhecimentos sobre as operações com os conjuntos, como a união, a intersecção e a diferença.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Dado o conjunto A e B, temos que A U B = {1, 2, 4, 6, 8, 10, 12, 14, 16}, que A – B = {1, 2, 10}, e que A ∩ B = {6, 8, 16}, assim, o conjunto B é igual a:
Alternativa E. Sabemos que A U B = {1, 2, 4, 6, 8, 10, 12, 14, 16}, além disso, sabemos que os elementos exclusivos de A, ou seja, elementos que pertencem ao conjunto A e não pertencem ao conjunto B, são A – B = {1, 2, 10}. Conhecemos também os elementos que pertencem aos dois conjuntos A ∩ B = {6, 8, 16}.
Então o conjunto B é composto pelos elementos da intersecção e pelos elementos que não pertencem ao conjunto A – B, são eles:
B = {4, 6, 8, 12, 14, 16}
-
Questão 2
Em uma escola de formação de condutores, constatou-se que todos os 34 alunos estavam tirando a primeira carteira nacional de habilitação (CNH). O professor perguntou quantos estavam ali para tirar a CNH da categoria A, e 12 estudantes levantaram a mão, posteriormente, ele perguntou quantos estavam ali para obter CNH da categoria B, e 29 levantaram a mão, sendo assim, a quantidade de candidatos que pretendem tirar somente a CNH da categoria A é:
Alternativa C. Sabemos que há um total de 34 alunos, mas que 29 deles estão tirando CNH para a categoria B e 12 estão tirando para a categoria A. Realizando a soma 29 + 12 = 41, note que há 7 a mais, pois 41 – 34 = 7, isso significa que há 7 alunos que pertencem à intersecção, ou seja, vão tirar as duas CNH. Sendo assim, para encontrar a quantidade de pessoas que vão tirar exclusivamente a CNH categoria A, basta subtrair 12 – 7 = 5
-
Questão 3
Em uma escola de idiomas que oferece formação para vários tipos de línguas, foi feita uma pesquisa para saber o número de estudantes matriculados em espanhol, inglês e alemão e outros idiomas. Os dados foram anotados na tabela a seguir:
Idioma
Quantidade
Inglês
110
Espanhol
84
Alemão
32
Inglês e Espanhol
30
Inglês e Alemão
20
Alemão e Espanhol
6
Inglês, Espanhol e Alemão
2
Outros
45
O total de alunos que participaram da pesquisa foi:
Alternativa B. Para encontrar o total de estudantes consultados, primeiro precisamos lembrar que, ao realizar a soma direta dos resultados da tabela, estaríamos contando mais de uma vez o mesmo estudante, pelo fato de existir interseção. Então sabemos que há a intersecção de todos os conjuntos, que, nesse caso, possui 2 elementos que pertencem aos três conjuntos ao mesmo tempo.
Posteriormente preenchemos com os elementos que pertencem somente a dois conjuntos ao mesmo tempo. Ao pegar os dados na tabela, é necessário realizar a subtração dos 2 elementos que já foram contados por pertencerem aos três conjuntos.
Inglês, Espanhol e Alemão
2
Somente Inglês e Espanhol
30 – 2 = 28
Somente Inglês e Alemão
20 – 2 = 18
Somente Alemão e Espanhol
6 – 2 = 4
Agora encontraremos os termos exclusivos, ou seja, que pertencem somente a um dos conjuntos. Nesse caso, é necessário realizar a subtração dos elementos que já foram contados, por exemplo, no de Inglês. Vamos subtrair todos os elementos das intersecções, ou seja, quem faz somente Inglês e Espanhol, quem faz somente Inglês e Alemão e quem faz os três cursos. Para Espanhol e Alemão, usamos o mesmo raciocínio, então teremos:
Somente Inglês
110 – 28 – 18 – 2 = 62
Somente Espanhol
84 – 28 – 4 – 2 = 50
Somente Alemão
32 – 18 – 4 – 2 = 8
Além desses valores, há 45 estudantes que escolheram outros.
Agora realizaremos a soma dos valores encontrados:
Total = 2 + 28 + 18 + 4 + 62 + 50 + 8 + 45 = 217
-
Questão 4
(PUC) Em um colégio, de 100 alunos, 80 gostam de sorvete de chocolate, 70 gostam de sorvete de creme e 60 gostam dos dois sabores. Quantos alunos não gostam de nenhum dos dois sabores?
Alternativa B. Sabemos que o total de alunos é igual a 100, e que dos 80 que gostam de chocolate, 60 gostam também de creme, então 80 – 60 = 20 que gostam somente de chocolate. Com esse mesmo raciocínio 70 – 60 = 10, então 10 gostam somente de creme. Sendo assim, vamos somar o total de alunos que gostam somente de chocolate, somente de creme e de ambos:
20 + 60 + 10 = 90
Como 100 alunos foram consultados, então 100 – 90 = 10.
10 não gostam de nenhum dos dois.
-
Questão 5
(UFSE) Os senhores A, B e C concorriam à liderança de certo partido político. Para escolher o líder, cada eleitor votou apenas em dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C, e 20 votos para A e C. Em consequência:
Alternativa E.
Vamos analisar a quantidade de votos que cada candidato recebeu:
A → n(AUB) = 100 e n(AUC) = 20
A = 100 + 20 = 120 votos
B → n(AUB) = 100 e n(BUC) = 80
B = 100 + 80 = 180 votos
C → n(AUC) = 20 e n(BUC) = 80
C = 20 + 80 = 100 votos
Analisando o total de votos, sabemos que o candidato B foi o mais votado.
-
Questão 6
(Mackenzie) Sendo A = {1, 2, 3, 5, 7, 8} e B = {2, 3, 7}, então o complementar de B em A é:
Alternativa E. O complementar de B em relação ao conjunto A são os elementos exclusivos do conjunto A, ou seja, A – B:
A – B = {1, 5, 8}
-
Questão 7
(Enem) No dia 17 de maio passado, houve uma campanha de doação de sangue em uma universidade. Sabemos que o sangue das pessoas pode ser classificado em quatro tipos quanto a antígenos. Uma pesquisa feita com um grupo de 100 alunos da universidade constatou que 42 deles têm o antígeno A, 36 têm o antígeno B, e 12 o antígeno AB. Sendo assim, podemos afirmar que o número de alunos cujo sangue tem o antígeno O é:
Alternativa C.
Sabendo que havia um total de 100 alunos, vamos encontrar o total de estudantes que possuem antígeno somente A, somente B e A∩B.
Sabemos que A∩B = 12
A – B (somente em A) = 42 – 12 = 30
B – A (somente em B) = 36 – 12 = 24
Somando temos um total de 12 + 30 + 24 = 66 estudantes, então os demais são O, como foram consultados 100 alunos:
100 – 66 = 34
-
Questão 8
Dado o conjunto A = {3, 4, 5, 6, 7, 8, 9, 10}, B = {9, 10, 11, 12} e C = {5, 7, 9, 11, 13}, os elementos do conjunto (A∩B)UC são:
Alternativa D.
Primeiro encontraremos A∩B.
A∩B = {9, 10}
Agora faremos a união de (A∩B)UC = {5, 7, 9, 10, 11, 13}
-
Questão 9
A seguir, há a representação de um diagrama formado pelo conjunto A e B.
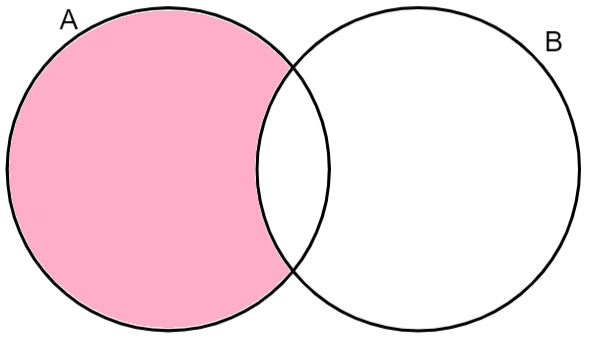
Analisando a imagem, podemos afirmar que a região destacada em rosa pode ser descrita por:
Alternativa C. A parte em destaque corresponde aos elementos que pertencem somente ao conjunto A.
-
Questão 10
Analisando os diagramas a seguir, assinale a alternativa que representa o conjunto (AUB) – (A∩B):
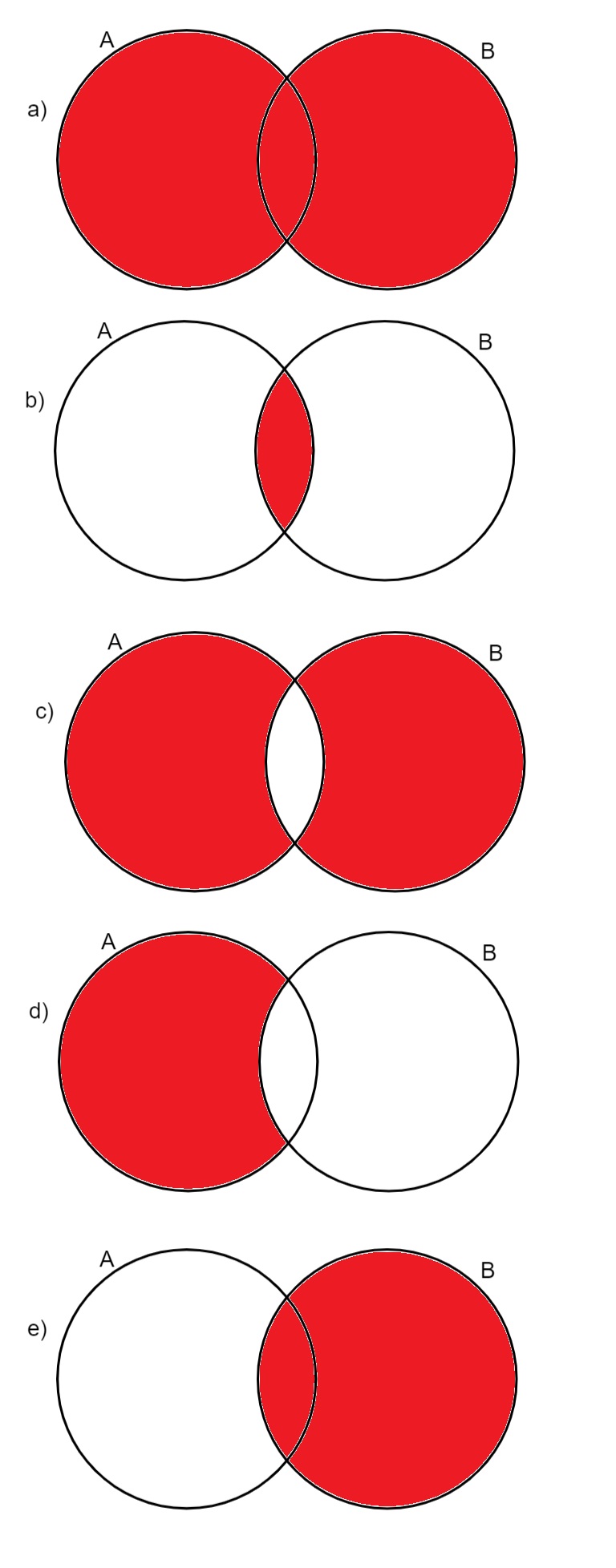
Alternativa C. Note que, em vermelho, estão os elementos que pertencem somente ao conjunto A e os elementos que pertencem somente ao conjunto B, e que somente a intersecção entre A e B não está em destaque.
-
Questão 11
Dados os conjuntos A, B e C, cujos termos possuem as seguintes características:
A → conjunto dos números pares
B → conjunto dos números ímpares
C → conjunto dos múltiplos de 4
Julgue as afirmativas a seguir:
I – A está contido em C.
II – C está contido em A.
III – A intersecção entre A e B é igual ao conjunto vazio.
Alternativa B
I → falsa, pois nem todo número múltiplo de 2 é múltiplo de 4.
II → verdadeira, pois todos os números múltiplos de 4 são múltiplos de 2.
III → verdadeira, pois não existe um número que seja ímpar e par simultaneamente.
-
Questão 12
Analise o diagrama a seguir:
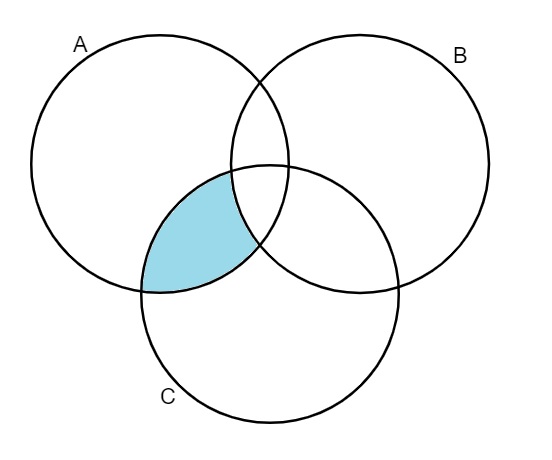
A região destacada em azul pode ser descrita pela operação:
Alternativa C. Analisando o diagrama, é possível perceber que a região em destaque corresponde à intersecção entre os conjuntos A e C menos os elementos que pertencem ao conjunto B.