Exercícios sobre os segmentos proporcionais
Sejam AB, BC, CD e DE segmentos de reta, com as respectivas medidas: 2, 4, 10 e 5. É possível dizer que esses segmentos são proporcionais?
a) Não, independentemente da ordem estabelecida entre eles.
b) Sim, se a ordem entre os segmentos for: AB, CD, BC e DE.
c) Sim, se a ordem entre eles for a mesma dada no enunciado.
d) Sim, se a ordem entre eles for AB, DE, BC e CD.
e) Nenhuma das alternativas.
a) Incorreta!
Se não fosse possível reordenar os segmentos, a resposta correta realmente seria não. Entretanto, o exercício abriu margem para reordená-los. Sendo assim, em outra ordem, os segmentos são proporcionais.
b) Incorreta!
Nessa ordem, teríamos:
2 = 4
10 5
0,2 = 0,8
O que é um resultado absurdo.
c) Incorreta!
Na ordem em que os segmentos foram apresentados no enunciado, teríamos:
2 = 10
4 5
0,5 = 2
O que é um resultado absurdo.
d) Correta!
e) Incorreta, pois a alternativa D é a que apresenta a ordem correta para os segmentos serem considerados proporcionais.
Gabarito: Letra D.
Os segmentos a seguir são proporcionais seguindo a ordem em que foram apresentados. A razão de proporcionalidade e o comprimento de x, em milímetros, são:
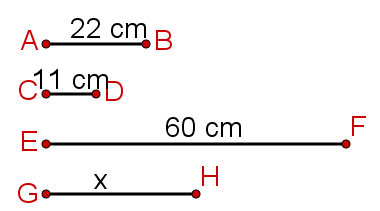
a) 2 e 30 milímetros.
b) 0,5 e 30 milímetros.
c) 2 e 300 milímetros.
d) 0,5 e 300 milímetros.
e) 30 e 300 milímetros.
Em primeiro lugar, construa a proporção:
22 = 60
11 x
A razão de proporcionalidade entre eles será a mesma, por isso, pode ser obtida já na primeira fração: 22/11 = 2. O valor de x pode ser obtido por meio da multiplicação cruzada:
22 = 60
11 x
22x = 60·11
22x = 660
x = 660
22
x = 30
Descobrimos que x mede 30 cm, mas o execício pede essa medida em milímetros, portanto:
30 cm = 30·10 mm = 300 mm
Gabarito: Letra C.
Os polígonos na imagem abaixo são semelhantes. Isso significa que seus lados correspondentes são proporcionais. Dadas essas informações, encontre a razão de proporcionalidade entre os lados do polígono ABCD e os lados do polígono EFGH e descubra os comprimentos de x e de y.
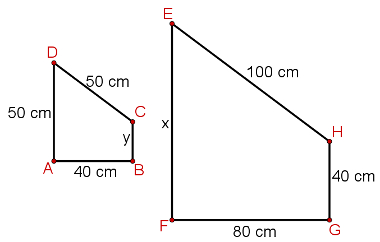
a) 2, 100 cm e 20 cm
b) 2, 20 cm e 100 cm
c) 2, 50 cm e 40 cm
d) 0,5; 20 cm e 100 cm
e) 0,5; 100 cm e 20 cm
Na ordem estabelecida, a razão de proporcionalidade é obtida dividindo a medida de um dos lados do primeiro polígono pelo lado correspondente a ele no segundo.
AB = 40 = 0,5
FG 80
Observando essa razão, podemos perceber que os lados do polígono EFGH medem o dobro de seus correspondentes no outro polígono. Assim sendo, x é o dobro de 50, e 40 é o dobro de y. A partir disso, seguem os resultados:
x = 100 cm e y = 20 cm.
Também é possível resolver esse exercício usando a propriedade fundamental das proporções, mas isso daria muito mais trabalho.
Gabarito: Letra E.
Quatro segmentos, AB, CD, EF e GH, são proporcionais nessa ordem. Sabendo que o comprimento do segmento AB é de 20 cm e que a razão de proporcionalidade é 2,5, calcule o comprimento do segmento CD.
a) 8 cm
b) 10 cm
c) 12 cm
d) 14 cm
e) 16 cm
Como temos o resultado da razão de proporcionalidade, para descobrir a medida do segmento CD, basta montar uma razão, igualar a razão de proporcionalidade e realizar os cálculos. Observe:
20 = 2,5
CD
2,5CD = 20
CD = 20
2,5
CD = 8 cm.
Gabarito: Letra A.
