Exercícios sobre os tipos de Funções
Analise o diagrama abaixo e determine: o domínio, o contradomínio e o conjunto imagem.
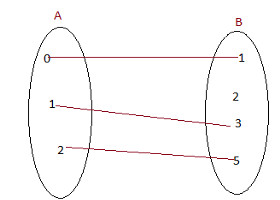
Pelo diagrama, temos:
Domínio: D (f) = {0, 1, 2}
Contradomínio: CD (f) = {1, 2, 3, 5}
Conjunto Imagem: Im (f) = {1, 3, 5}
Essa função é definida por: 2x +1
Observe que não há nenhum elemento x em A, que substituindo em 2x + 1 resulta em 2. Por isso não teve associação.
Defina a função abaixo e classifique-a em injetora, sobrejetora ou bijetora.
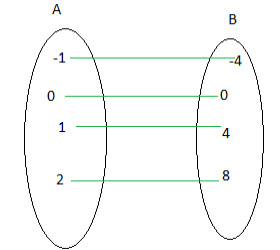
A função é definida por:
F(x) = 4x
Veja: 4 . (-1) = -4
4 . (0) = 0
4 . 1 = 4
4 . 2 = 8
A Função é injetora, pois os elementos distintos do domínio têm imagens distintas. Além disso, a função é sobrejetora pois o contradomínio é igual à imagem. Deste modo, a função é bijetora.
Marque a alternativa que representa a função abaixo:
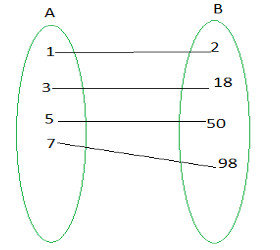
a) f(x) = 2x + 2; Bijetora
b) f(x) = x² + 2; Injetora
c) f(x) = 2x²; Sobrejetora
d) f(x) = 2x²; Bijetora
e) f(x) = x²; Injetora
A função é definida por F(x) = 2x²
Funções que como essa são tanto sobrejetoras quanto injetoras, são classificadas como funções bijetoras.
Dada a função f:R →R definida por: f(x) = x². Determinar f(0), f(-1), f (-2), f(1), f(2) e o tipo de função.
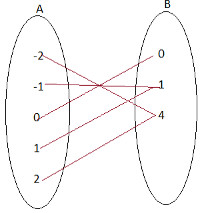
f(0) = 0 ² = 0
f (-1) = (-1)² = 1
f (1) = 1² = 1
f (-2) = (-2)² = 4
f (2) = 2² = 4
A função não possui classificação, pois não é injetora nem sobrejetora.
