Exercícios sobre perímetro
Definimos como perímetro:
A) a medida da superfície de uma figura plana.
B) a capacidade de um sólido geométrico.
C) o comprimento de uma das dimensões de uma figura plana.
D) o comprimento do contorno de uma figura plana.
E) o espaço ocupado por um sólido geométrico.
Alternativa D
O perímetro é o comprimento do contorno de uma figura plana.
A seguir está uma representação do terreno de Jorge, com as medidas de cada um dos lados.
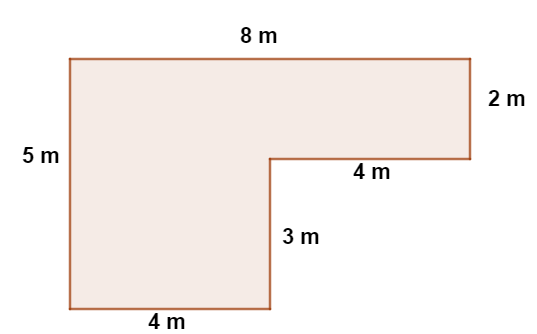
Analisando esse terreno, podemos afirmar que o seu perímetro é de:
A) 16 metros
B) 20 metros
C) 24 metros
D) 26 metros
E) 30 metros
Durante um treino de futebol, o técnico pediu para que os jogadores dessem 12 voltas correndo em torno do gramado. Sabendo que o campo possui 98 metros de largura e 72 metros de comprimento, a distância percorrida pelos atletas foi igual a:
A) 4080 m
B) 2040 m
C) 1020 m
D) 510 m
E) 340 m
Alternativa A
Como o campo de futebol é retangular, dois lados medem 72 metros e os outros dois, 98 metros. Primeiramente, calcularemos o perímetro:
\(P = 72 + 72 + 98 + 98\)
\(P = 340 metros\)
Agora, faremos a multiplicação por 12:
\(340\cdot12=4080\ m\)
Um heptágono regular possui perímetro igual a 87,5 metros, então podemos afirmar que a medida do lado desse heptágono é de:
A) 12,0 metros
B) 12,5 metros
C) 13,0 metros
D) 13,5 metros
E) 14,0 metros
Alternativa B
Como o polígono é regular, os seus lados são congruentes. Assim, para calcular a medida do lado, basta dividirmos o perímetro pelo número de lados.
87,5 : 7 = 12,5 metros
Para cercar o terreno a seguir, Matias optou por colocar uma cerca que tem um custo de R$ 3,00 o metro:
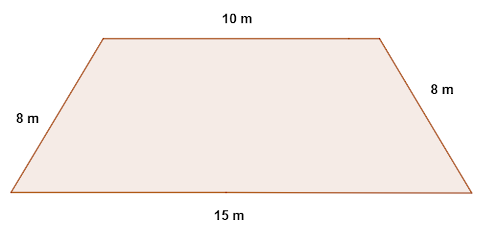
O valor gasto para cercar todo o terreno de Matias é:
A) R$ 46,00
B) R$ 110,00
C) R$ 125,00
D) R$ 138,00
E) R$ 161,00
Alternativa D
Como cada metro custa R$ 3,00, o valor gasto para cercar o terreno é calculado por:
46⋅3,0 = 138
Em um forro de mesa que possui 1,10 m de largura e 1,40 metros de comprimento será feito um bordado. Em quantos metros desse forro de mesa, no mínimo, foi feito esse bordado?
A) 1 metro
B) 2 metros
C) 3 metros
D) 4 metros
E) 5 metros
Alternativa E
Calculando o perímetro de um retângulo, temos que:
\(P=2\ \left(1,1+1,4\right)\)
\(P=2\cdot2,5\ \)
\(P=5\ metros\ \)
A tela de um televisor está em uma razão de 4 para 3. Se o perímetro do televisor é de 280 cm, então ele possui área igual a:
A) 3600 cm²
B) 4800 cm²
C) 5400 cm²
D) 6200 cm²
E) 6400 cm²
Alternativa B
Como o perímetro desse televisor é de 280 cm:
\(P=2\ \left(4x+3x\right)\)
\(P=2\cdot7x\)
\(P=14x\)
\(280=14x\)
\(x=\frac{280}{14}\)
\(x=20\ \)
Sabendo que x é igual a 20:
\(4x=4\cdot20=80\ \)
\(3x=3\cdot20=60\ \)
Para calcular a área, multiplicamos a base pela altura:
\(A=80\cdot60\ \)
\(A=4800\ cm^2\)
Mariana decidiu separar parte do seu terreno para o plantio de plantas medicinais. Como o seu quintal não é muito grande, ela separou uma área quadrada de 4 m² para a horta. Caso ela decida colocar uma cerca nesse terreno, a quantidade de metros que essa cerca deve ter, no mínimo, é igual a:
A) 4 metros
B) 6 metros
C) 8 metros
D) 10 metros
E) 12 metros
Alternativa C
Como a área do terreno é de 4 metros quadrados, e ele possui formato de um quadrado, considerando que a área do quadrado é l²:
\(l^2=4\)
\(l=\sqrt4\)
\(l=2\)
Como a medida do lado é 2 metros, e o quadrado possui 4 lados congruentes, para calcular o perímetro, temos que:
\(P=4\cdot2\ \)
\(P=8\ metros\ \)
Para cercar o perímetro de uma região, constatou-se que ela possui o formato de um triângulo retângulo. Sabendo que os catetos desse triângulo medem 24 e 32 metros, o perímetro dessa região mede:
A) 40 metros
B) 56 metros
C) 80 metros
D) 96 metros
E) 124 metros
Alternativa D
Para calcular o perímetro dessa região que possui formato de triângulo retângulo, primeiramente utilizaremos o teorema de Pitágoras para calcular o comprimento da hipotenusa, representado por x:
\(x^2={24}^2+{32}^2\)
\(x^2=576+1024\)
\(x^2=1600\)
\(x=\sqrt{1600}\)
\(x=40\ metros\)
Como a hipotenusa mede 40 metros, o perímetro dessa região mede:
\(P = 40 + 24 + 32 = 96 metros\)
Em um retângulo, a largura mede a metade do seu comprimento. Sabendo que o seu perímetro é de 18 cm, a medida do comprimento desse retângulo é igual a:
A) 3 cm
B) 5 cm
C) 6 cm
D) 10 cm
E) 12 cm
Alternativa C
Sendo x a medida da largura, o comprimento medirá 2x:
\(2x+2x+x+x=18\)
\(6x=18\)
\(x=\frac{18}{6}\)
\(x\ =\ 3\)
Como a largura mede 3, a medida do comprimento será o dobro da medida da largura, ou seja:
\(2x=2\cdot3=6\ cm\)
Para cercar um terreno retangular foi gasto um total de 38 metros de cerca. Sabendo que a largura desse terreno é de 7 metros, o comprimento do terreno é de:
A) 8 metros
B) 9 metros
C) 10 metros
D) 11 metros
E) 12 metros
Alternativa E
Sendo x a medida do comprimento do terreno, utilizando o valor conhecido do perímetro, temos que:
\(P = 7 + 7 + x + x\)
\(38 = 14 + 2x\)
\(38 – 14 = 2x\)
\(24 = 2x\)
\(x = \frac{24}{2}\)
\(x = 12 metros\)
(Saeb) A figura abaixo representa um terreno.
Podemos afirmar que seu perímetro vale
A) 46 m
B) 58 m
C) 92 m
D) 104 m
E) 120 m
Alternativa C
Calculando o perímetro:
\(P=12+10+12+12+12+12+12+10\)
\(P=92\ m\)
