Exercícios sobre Permutação de Números e Letras
U.F.Pelotas – RS
Tomando como base a palavra UFPEL, resolva as questões a seguir.
a) Quantos anagramas podem ser formados de modo que as vogais estejam sempre juntas?
b) Quantos anagramas podem ser formados com as letras PEL juntas nesta ordem?
a) Na palavra UFPEL, que possui 5 letras, temos duas vogais (U,E). Segundo o exercício, deveremos ter estas vogais sempre juntas, restando 3 letras para combinarmos com estas vogais.
Com isso, se permutarmos estas 3 consoantes (F,P,L), teremos;
P3 = 3! = 3.2.1 =6
Como são duas vogais, teremos duas maneiras de permutá-las entre si (UE ou EU), entretanto devemos verificar as possíveis posições destas vogais na palavra.
_____ _____ _____ _____ _____
Como as vogais têm que estar juntas, consideraremos uma só letra. Sendo assim, ao invés de termos 5 letras, as vogais se tornarão uma só, com isso, teremos 4 letras.
_____ _____ _____ _____, sendo que as vogais poderão ocupar qualquer um desses 4 espaços, ou seja, existem 4 possibilidades para as vogais aparecerem nas combinações.
Uma outra forma de analisar essa possibilidade para as vogais, seria descrever os possíveis casos.
U _ __E _ _____ _____ _____;
_____ U _ E _ _____ _____;
_____ _____ U _ E _ _____;
_____ _____ _____ U _ E _;
Ou seja, 4 possibilidades.
Finalizando as contas teremos a seguinte expressão para as possibilidades.
Possibilidades = 4.P2 .P3
P3 = Permutação das letras (FPL) ; P2 = Permutação das vogais (U,E)
Possibilidades = 4.P2 .P3 = 4.2.3 = 48
b) As letras PEL tornam-se uma única palavra, sem permutação entre as letras, pois elas devem estar juntas e na mesma ordem, restando apenas UF para permutarmos.
Devemos, então, calcular quantas maneiras diferentes teremos para combinar as letras PEL em toda a palavra.
PEL ____ ____
____ PEL ____
____ ____ PEL
Ou seja, há três combinações para as letras PEL nesta palavra.
Possibilidades = 3.P2
P2 = Permutação das letras (UF)
Possibilidades = 3 .P2 = 3.2 = 6
Temos então 6 possibilidades.
Um engenheiro de software deseja criar um programa que teste todas as possibilidades de senha de um sistema de uma empresa. A informação que este engenheiro tem é a de que esta senha precisa respeitar a seguinte sequência: quatro letras distintas seguidas por dois algarismos distintos. Sendo assim, responda:
a) Quantas são as possíveis senhas de acesso?
b) Quantas senhas apresentam simultaneamente apenas consoantes e algarismos maiores que 5?
a) Neste caso não permutaremos todas as letras, pois não temos esse espaço, afinal a senha possui apenas 4 dígitos formados por letras. Isto vale também para os números. Portanto, utilizaremos o caso geral da permutação, que é o Arranjo.
Lembre-se:
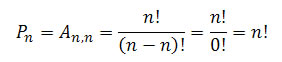
Para as letras, temos:
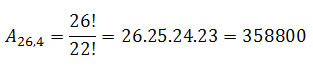
Para os números, temos:
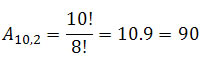
Com isso,as possíveis senhas serão dadas pelas multiplicações das possibilidades acima.
Senhas = 358800.90 = 32292000 possibilidades
b) Agora temos restrições para as letras e para os números. Letras: apenas consoantes; e números: somente aqueles maiores que 5.
Teremos, então, 21 possíveis letras para as senhas e 4 números (6,7,8,9).
Com isso, nossa senha ficará da seguinte forma.
Para as letras, temos:
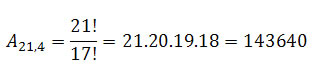
Para os números, temos:
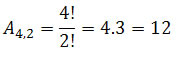
Dessa forma,as possíveis senhas serão dadas pelas multiplicações das possibilidades acima.
Senhas = 143640.12 = 1723680 possibilidades
Um banco adquire um cofre com um sistema de segurança digital, cuja senha para sua abertura é de 6 dígitos. Sabendo que estes dígitos podem ser letras ou números distintos, responda:
a) Quantas possíveis senhas podem ser formadas?
b) Quantas senhas podem ser formadas tendo três vogais nos primeiros dígitos?
a) Nosso campo de possibilidades para os dígitos é um total de 36 caracteres (26 letras e 10 números). Tratando-se de 6 dígitos, faremos os arranjos para esta senha.
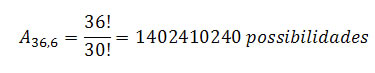
b) Temos que os três primeiros dígitos devem ser vogais, ou seja, combinaremos as 5 vogais em três dígitos.
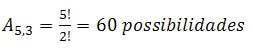
Para os outros 3 dígitos teremos os 36 possíveis caracteres, menos as vogais utilizadas, ou seja, 36-3 = 33 possíveis caracteres para a senha.
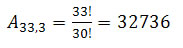
Com isso,as possíveis senhas serão dadas pelas multiplicações das possibilidades acima.
Senha s= 60.32736 = 1964160 possibilidades
Os produtos de uma empresa são armazenados no banco de dados com um código de 4 letras maiúsculas seguidas por 5 algarismos. Esse sistema será modificado para permitir letras maiúsculas e minúsculas. Após essa modificação, o número atual de códigos será multiplicado por:
a) 2
b) 6
c) 10
d) 18
e) 16
Vamos construir o sistema de contagem deste código.
26 possibilidades para as letras
10 possibilidades para os números.
O código será da seguinte forma:
LETRA LETRA LETRA LETRA Nº Nº Nº Nº Nº.
Com a nova formação do código podendo ser maiúscula ou minúscula, cada letra da senha terá duas possibilidades (maiúscula ou minúscula). Denotaremos esta possibilidade por (2p):
LETRA (2p) LETRA (2P) LETRA (2p) LETRA (2p) Nº Nº Nº Nº Nº.
Sabemos que se formos calcular as possibilidades, devemos multiplicar a possibilidade de cada dígito. O diferencial entre o código antigo e o novo são as novas possibilidades para cada letra, ou seja, a diferença de possibilidades entre o antigo e o novo estará no resultado das novas possibilidades.
Possibilidade para os quatro primeiros dígitos do código antigo:
Possibilidade antiga = A(26,4) = 26letras.25letras.24letras.23letras
Possibilidade para os quatro primeiros dígitos do código novo:
Possibilidade das letras = 26 letras .(2).25letras.(2).24letras.(2).23letras.(2)
Possibilidade das letras = (2).(2).(2).(2).26 letras .25letras.24letras.23letras
Possibilidade das letras = 16.(Possibilidade antiga)
Como os números não mudam, a possibilidade do novo código será:
Novo código = 16.26letras.25letras.24letras.23letras.10números.9números
Ou seja, o número atual de códigos será multiplicado por 16 em relação ao antigo.
Vunesp - SP
Considere todos os números formados por seis algarismos distintos obtidos permutando-se, de todas as formas possíveis, os algarismos 1, 2, 3, 4, 5, 6.
a) Determine quantos números podemos formar (no total) e quantos números são iniciados com o algarismo 1.
b) Escrevendo-se esses números em ordem crescente, determine qual posição ocupa o número 512346 e que número ocupa a 242ª posição.
a) Fixaremos o número 1 no primeiro algarismo, permutando os demais. Dessa forma, teremos 5 números para permutarmos em 5 casas.
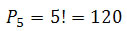
b) Deveremos calcular quantos números tem em cada casa, na ordem.
Para o primeiro algarismo igual a 1, já temos 120 números.
Para o primeiro algarismo igual a 2, teremos também 120 números.
Para o primeiro algarismo igual a 3, teremos 120 números.
Para o primeiro algarismo igual a 4, teremos 120 números.
O primeiro número após os algarismos, com a primeira casa igual a 4, será o primeiro número da ordem de números com primeiro algarismo igual a 5.
E será o número 512346.
Ou seja, esse número ocupa a posição 481º.
Agora vamos encontrar o número que ocupa a 242ª posição. Vimos que até a 240ª posição são números formados pelos algarismos 1 e 2 na primeira posição, sendo que o número que ocupa a 241ª posição inicia-se com o algarismo 3 na primeira posição.
241ª = 312456
242ª = 312465
Neste caso foi fácil encontrar o número escrevendo-o, pois a posição encontrava-se próxima à mudança de algarismo.
