Exercícios sobre pirâmide
Pirâmides são sólidos geométricos estudados na geometria espacial. Esse sólido possui elementos importantes e fórmulas específicas para calcular a área total e o volume.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Uma pirâmide possui base formada por um triângulo retângulo que tem catetos medindo 6 centímetros e 8 centímetros e altura igual a 10 centímetros. Então, o volume dessa pirâmide, em cm³, é igual a:
Alternativa E
Primeiro calcularemos a área da base da pirâmide. Como ela é um triângulo retângulo, calculamos a área multiplicando a base pela altura e dividindo por dois
Ab = b · h : 2
Ab = 6 · 8 : 2
Ab = 48 : 2
Ab = 24
Agora calcularemos o volume da pirâmide.
-
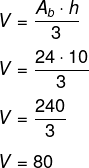
Questão 2
Uma pirâmide reta possui base quadrada, com 6 metros de lado e altura igual a 4 metros. Sabendo disso, podemos afirmar que o comprimento da sua geratriz é igual a:
Alternativa B
Para facilitar a resolução, vamos representar a geratriz:
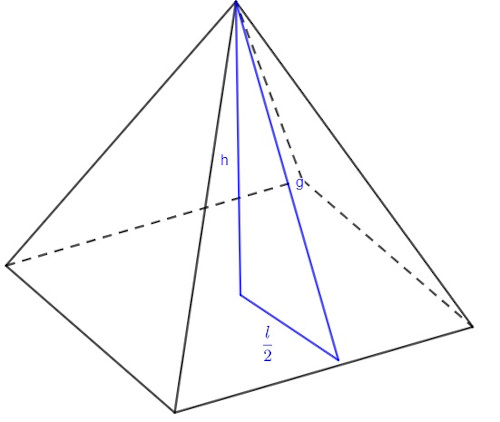
Sabemos que a metade do lado é 6 : 2 = 3.
Então:
l/2 = 3
h = 4
Pelo teorema de Pitágoras, temos que:
g² = 3² + 4²
g² = 9 + 16
g² = 25
g = √25
g = 5
-
Questão 3
A geratriz de uma pirâmide reta é de 25 cm. Sabendo a distância da projeção da altura na base até o lado da pirâmide, que é de 7 cm, então, a altura da pirâmide é de:
Alternativa D
Seja d a distância da projeção da altura na base até o lado da pirâmide, para encontrar a altura, basta aplicar o teorema de Pitágoras.
g² = h² + d²
25² = h² + 7²
625 = h² + 49
625 – 49 = h²
576 = h²
h = √576
h = 24
-
Questão 4
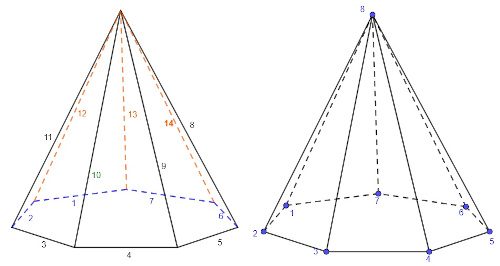
Analisando as pirâmides a seguir, julgue as afirmativas:
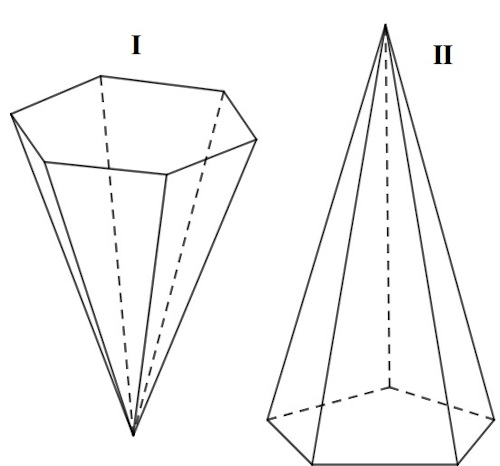
1. As pirâmides I e II são, respectivamente, pirâmide de base hexagonal e pirâmide de base pentagonal.
2. A pirâmide I possui 12 arestas, já a pirâmide II possui 10 arestas.
3. A pirâmide I possui 6 vértices, já a pirâmide II possui 5 vértices.
Marque a alternativa correta:
Alternativa D
1. Verdadeira. Basta verificar que a base da pirâmide I é um hexágono e que a base da pirâmide II é um pentágono.
2. Verdadeira. Realizando contagem das arestas, as pirâmides possuem, respectivamente, 12 e 10 arestas.
3. Falsa. A pirâmide I possui 7 vértices, e a pirâmide II, 6.
-
Questão 5
O octaedro é um sólido geométrico formado pela união de duas pirâmides, como na imagem a seguir:
Sabendo que a distância do vértice da pirâmide superior até o vértice da pirâmide inferior é de 24 cm, e que os lados do quadrado que é o encontro das duas pirâmides têm 8 cm, qual é o volume desse sólido geométrico?
Alternativa D
Como a base é um quadrado, então, a área da base é dada por l².
Ab = 8²
Ab = 64
A distância entre os vértices das pirâmides é de 24 cm, o que significa que cada pirâmide tem 12 cm de altura. Como há duas pirâmides, vamos calcular o volume de uma e multiplicar por dois.
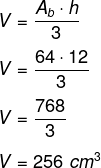
Como queremos o volume de duas pirâmides temos que:
2V = 2 · 256 = 512 cm³ -
Questão 6
A soma do número de vértices e arestas que uma pirâmide de base heptagonal possui é:
Alternativa C
Fazendo a representação dessa pirâmide, temos que:
Há um total de 14 arestas e 8 vértices. A soma é 14 + 8 = 22.
-
Questão 7
Uma embalagem, no formato de uma pirâmide com base quadrada, está sendo produzida por uma fábrica. Sabendo que a geratriz dessa embalagem tem 30 cm, e que o lado da base mede 12 cm, a área total dessa pirâmide é de:
Alternativa A
Para calcular a área total, calcularemos a área da base e a área lateral.
Como a base é um quadrado, temos que:
Ab = l²
Ab = 12²
Ab = 144 cm²
A lateral da pirâmide de base quadrada é composta por 4 triângulos, de altura igual a 30 cm e base igual a 12 cm. Sabemos que a área do triângulo é igual à base vezes a altura dividido por 2.
Al = 4 · 12 · 30 : 2
Al = 720 cm²
A área total é de:
AT = 144 + 720 = 864 cm²
-
Questão 8
Julgue as afirmativas a seguir sobre pirâmides:
I – O cone é uma pirâmide de base circular.
II – Toda pirâmide é um poliedro.
III – Dados um prisma e uma pirâmide com mesma altura e mesma área da base, o volume do prisma é o triplo do volume da pirâmide.
São verdadeiras:
-
Questão 9
(Enem) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
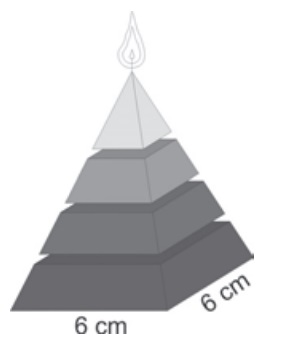
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
Alternativa B
Para encontrar o volume da nova pirâmide, vamos calcular a diferença entre o volume da pirâmide maior e o volume da pirâmide menor. Note que há 1 cm de distância entre os blocos, então, a altura da pirâmide maior é 19 – 3 = 16 cm. A pirâmide maior tem 6 cm de lado da base, como a base é um quadrado, então, Ab = l² = 6² = 36.
Calculando o volume da pirâmide maior, temos que:
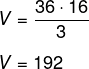
A altura da pirâmide menor na parte superior é 16 : 4 = 4, e a aresta é 6 : 4 = 1,5. Assim, a área da base dessa pirâmide menor é 1,5² = 2,25. Calculando o volume, temos que:
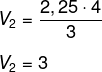
A diferença entre os volumes é 192 – 3 = 189.
-
Questão 10
(Enem 2021) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são
-
Questão 11
(Enem 2019) As luminárias para um laboratório de matemática serão fabricadas em forma de sólidos geométricos. Uma delas terá a forma de um tetraedro truncado. Esse sólido é gerado a partir de secções paralelas a cada uma das faces de um tetraedro regular. Para essa luminária, as secções serão feitas de maneira que, em cada corte, um terço das arestas seccionadas serão removidas. Uma dessas secções está indicada na figura.
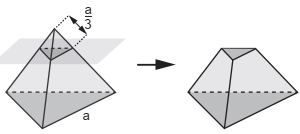
Essa luminária terá por faces:
Alternativa A
Analisando a imagem da luminária após as secções:
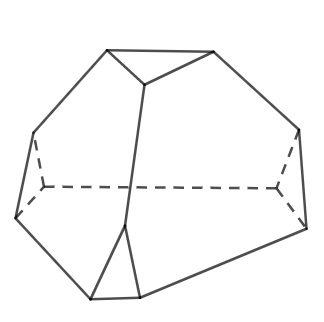
As faces formadas são 4 triângulos equiláteros e 4 hexágonos.
-
Questão 12
Uma fábrica decidiu fazer mudanças em sua embalagem de perfume. A embalagem antes era formada por um prisma de base hexagonal, e tinha a capacidade de 360 ml. Uma nova embalagem será feita com a mesma base, mesma altura, mas no formato de uma pirâmide. O volume dessa nova base será de:
Alternativa C
Como a altura e a base são as mesmas, sabemos que o volume do prisma é dado por:
Vprisma = Ab · h
Já o volume da pirâmide é calculado por:
Vpirâmide = Ab · h : 3
Note que o volume da pirâmide é 1/3 do volume do prisma, então, basta dividir o volume do frasco por 3.
360 : 3 = 120 ml
