Exercícios sobre polígonos
Esta lista traz exercícios sobre os polígonos, que são estudados na geometria plana. É fundamental compreender o que é um polígono e quais são os seus principais elementos.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O polígono que possui o mesmo número de diagonal e de lados é um:
A) triângulo.
B) quadrilátero.
C) pentágono.
D) hexágono.
E) dodecágono.
Alternativa C
Encontraremos o polígono em que n = d. Utilizando a fórmula da diagonal: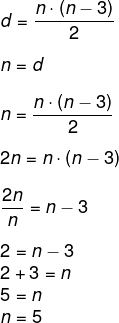
O polígono que possui 5 lados é o pentágono.
-
Questão 2
Julgue as afirmativas a seguir:
I → Todo polígono possui diagonal.
II → A soma dos ângulos internos de um quadrilátero é sempre igual a 360º.
III → O dodecágono é um polígono de 12 lados.
Marque a alternativa correta:
A) Todas as afirmativas são verdadeiras.
B) Somente a afirmativa I é falsa.
C) Somente a afirmativa II é falsa.
D) Somente a afirmativa III é falsa.
E) Todas as afirmativas são falsas.
Alternativa B
I → falsa
O triângulo não possui diagonal.
II → verdadeira
Calculando a soma dos ângulos internos de um quadrilátero:
Si = (n – 2) · 180º
Si = (4 – 2) · 180º
Si = 2 · 180º
Si = 360º
III → verdadeiro
Dodecágono é o nome dado para um polígono de 12 lados.
-
Questão 3
A face superior de uma determinada peça de um automóvel possui formato de um polígono regular que possui ângulos internos medindo 120º cada. Sendo assim, podemos afirmar que o número de lados que essa face possui é igual a
A) 4.
B) 5.
C) 6.
D) 7.
E) 8.
-
Questão 4
Em um determinado polígono, o número de diagonais é igual a oito vezes o número de lados, então, esse polígono é o:
A) eneadecágono
B) dodecágono
C) icoságono
D) decágono
E) octógono
Alternativa A
Temos que n = 8d. Utilizando a fórmula da diagonal, temos que:
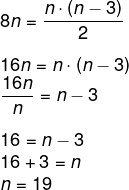
O polígono com 19 lados é um eneadecágono.
-
Questão 5
Durante a elaboração de móveis planejados, um marceneiro recebeu uma encomenda para que fosse feita uma mesa de madeira idêntica à da imagem a seguir:

Ao analisar o polígono que forma a face superior da mesa, a soma dos seus ângulos internos é igual a:
A) 540°
B) 720°
C) 800°
D) 1080°
E) 360°
Alternativa D
Como o polígono da face da mesa possui 8 lados, então, temos que:
Si = (n – 2) · 180°
Si = (8 – 2) · 180°
Si = 6 · 180°
Si = 1080°
-
Questão 6
Os ângulos internos de um pentágono medem 2x – 10, 4x + 10, 3x + 10, 6x + 30 e 5x. Então, podemos afirmar que a medida do menor ângulo desse polígono é:
A) 40º
B) 45º
C) 50º
D) 55º
E) 62º
Alternativa A
A soma dos ângulos internos de um pentágono pode ser calculada por:
Si = (n – 2) · 180°
Si = (5 – 2) · 180°
Si = 3 · 180°
Si = 540°
Sabendo que a soma dos ângulos internos é 540°, então, temos que:
2x – 10 + 4x + 10 + 3x + 10 + 6x + 30 + 5x = 540
20x + 40 = 540
20 x = 540 – 40
20x = 500
x = 500 : 20
x = 25
Sabendo que x = 25, o menor ângulo é 2x – 10:
2 · 25 – 10 = 50 – 10 = 40º
-
Questão 7
(Excelência 2018) Ana ganhou um presente em forma de polígono e só poderia abrir se descobrisse quantos lados têm esse polígono. Sabendo que a soma dos ângulos internos desse polígono é igual a 2340º, quantos lados têm esse polígono?
A) 20 lados
B) 15 lados
C) 10 lados
D) nenhuma das alternativas
Alternativa B
Sabemos que Si = 2340.
Então, temos que:
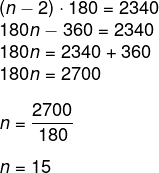
-
Questão 8
Em um polígono regular, a soma dos ângulos internos é 1620º. Então, o número de diagonais que esse polígono tem é:
A) 11
B) 22
C) 35
D) 44
E) 58
Alternativa D
Primeiro encontraremos o número de lados desse polígono:
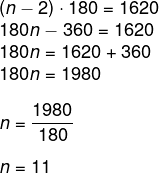
Como esse polígono possui 11 lados, calcularemos agora o número de diagonais:
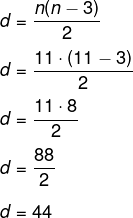
-
Questão 9
No polígono a seguir, sabendo que ele é regular, o valor do ângulo α é:
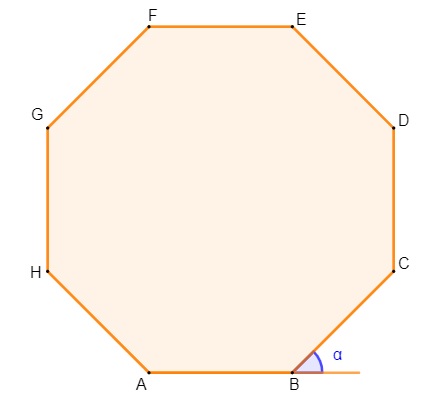
A) 20º
B) 30º
C) 35º
D) 40º
E) 45º
Alternativa E
Sabemos que o ângulo externo é suplementar ao ângulo interno, ou seja, a soma dos dois é igual a 180º. Primeiro encontraremos o valor do ângulo interno. Como esse polígono possui 8 lados, então, temos que:
Si = (n – 2) · 180º
Si = (8 – 2) · 180º
Si = 6 · 180º
Si = 1080º
Como se trata de um polígono regular, para encontrar a medida de cada ângulo, basta dividir 1080 : 8 = 135º.
Se um ângulo interno mede 135º, então, o seu suplementar mede α = 180 – 135 = 45º.
-
Questão 10
(PUC-RJ) Os ângulos internos de um quadrilátero medem 3x – 45, 2x + 10, 2x + 15 e x + 20 graus. O menor ângulo mede:
A) 90°
B) 65°
C) 45°
D) 105°
E) 80°
Alternativa B
A soma dos ângulos internos de um quadrilátero é sempre igual a 360º, então, temos que:
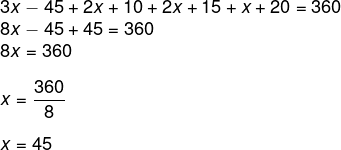
Então, os ângulos são:
3x – 45 = 3 · 45 – 45 = 90
2x + 10 = 2 · 45 + 10 = 100
2x + 15 = 2 · 45 + 15 = 105
x + 20 = 45 + 20 = 65
O menor ângulo mede 65º.
-
Questão 11
Classifique os polígonos a seguir como côncavo ou convexo:
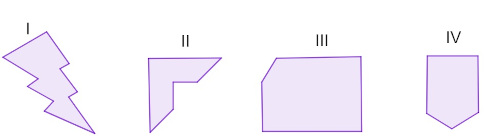
Os polígonos são, respectivamente:
A) convexo, convexo, côncavo e côncavo.
B) côncavo, convexo, côncavo e convexo.
C) convexo, convexo, convexo e côncavo.
D) côncavo, côncavo, convexo e convexo.
E) côncavo, côncavo, côncavo e convexo.
Alternativa D
Analisando os polígonos, temos que:
I → côncavo
II → côncavo
III → convexo
IV → convexo
-
Questão 12
Sobre os polígonos, julgue as afirmativas a seguir:
I → Um polígono é uma figura plana fechada por poligonais.
II → O círculo é um exemplo de polígono.
III → O segmento que liga dois vértices de um polígono é conhecido como diagonal.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Alternativa A
I → Verdadeira, pois essa é a definição de polígono.
II → Falsa, a circunferência não é fechada por poligonais, portanto, não é considerada um polígono.
III → Falsa, pois somente segmentos que ligam dois vértices não consecutivos formam diagonais.
Caso os vértices sejam consecutivos, o segmento formará um lado do polígono.