Exercícios sobre pontos gerais da Geometria Analítica
Quando duas retas são paralelas, o que se pode concluir a respeito de suas projeções ortogonais sobre um plano qualquer?
a) São retas transversais.
b) São retas paralelas.
c) São retas coincidentes.
d) São retas em planos distintos.
e) São retas perpendiculares.
A projeção ortogonal de duas retas paralelas sobre um plano será outras duas retas paralelas no plano, ou dois pontos, no caso particular em que essas retas contêm ponto do plano e são ortogonais a ele. Portanto, essas projeções ortogonais são retas paralelas.
Gabarito: Letra B.
Qual é a distância aproximada, em metros, entre o armazém A e a padaria B, sabendo que as suas coordenadas no mapa são dadas pelas coordenadas do ponto A (2,4) e do ponto B (3, -8)?
a) 40,4 m
b) 50,4 m
c) 12,3 m
d) 11,4 m
e) 12,4 m
A distância entre dois pontos é dada pela seguinte fórmula:
dAB = √[(x2 – x1)2 + (y2 – y1)2]
Substituindo as coordenadas dos pontos na fórmula, teremos:
dAB = √[(3 – 2)2 + ( – 8 – 4)2]
dAB = √[(1)2 + ( – 12)2]
dAB = √[1 + 144]
dAB = √145
dAB ≈ 12,04 m
Gabarito: Letra E.
A distância de um ponto P a um plano α é 8 cm e sua projeção ortogonal P' sobre α é o centro de um círculo contido nesse plano. Qual é a área do círculo e a do triângulo, respectivamente, sabendo que a distância de P a qualquer ponto da circunferência é 10 cm?
a) 36π cm2 e A = 24 cm2
b) 36 cm e A = 24 cm
c) 36 cm2 e A = 24 cm2
d) 24π cm2 e A = 24 cm2
e) 36π cm2 e A = 36 cm2
Primeiramente desenhe um esquema do enunciado acima e coloque as distâncias em seus respectivos lugares.
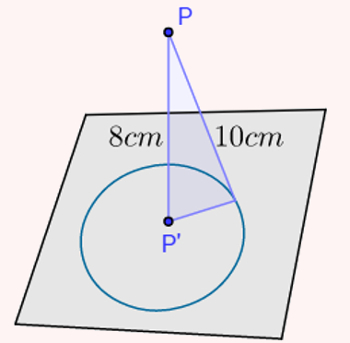
Note que o segmento de reta PP' é ortogonal (forma um ângulo de 90°) ao plano. Isso acontece porque P' é a projeção ortogonal de P. Dessa maneira, descobrindo a distância de P' até a borda da circunferência, descobrimos também a base do triângulo retângulo formado, que, ao mesmo tempo, é raio do círculo. Para isso, utilizaremos o Teorema de Pitágoras.
102 = 82 + x2
100 = 64 + x2
100 – 64 = x2
36 = x2
x = 6
Para calcular a área desse triângulo, cuja altura é 8 cm e a base é 6 cm, basta utilizar a fórmula:
A = b·h
2
A = 6·8
2
A = 48
2
A = 24 cm2
Já a área do círculo é dada pela fórmula:
A = πr2
A = π62
A = 36π cm2
Gabarito: Letra A.
(Fatec – SP) Assinale a alternativa verdadeira.
a) Três retas que, duas a duas, não têm ponto em comum são paralelas.
b) Dadas duas retas paralelas distintas, por uma delas passa um, e somente um, plano paralelo à outra reta.
c) por um ponto de uma reta pode-se traçar uma, e somente uma, perpendicular à reta considerada.
d) Por um ponto não pertencente a um plano pode-se traçar mais de uma reta paralela ao plano considerado.
e) Três pontos determinam um único plano.
a) Falsa!
Três retas que não possuem ponto em comum podem ser paralelas ou reversas. Para saber se são paralelas ou reversas, deve ser feita a projeção de uma das retas sobre o plano da segunda e observar se essa projeção é paralela ou transversal. Se for transversal, então as retas em cada plano serão reversas.
b) Falsa!
Dadas duas retas paralelas distintas, existem infinitos planos que passam por uma delas e que são paralelos à outra reta.
c) Falsa!
Lembre-se de que estamos considerando a geometria espacial. A partir dela, construa o plano A, perpendicular à reta dada, passando pelo ponto B em questão. São infinitas as retas nesse plano perpendicular à reta dada que contêm o ponto B. Logo, são infinitas as retas perpendiculares a essa reta passando por um de seus pontos.
d) Verdadeira!
Imagine que o plano dado chama-se A e o ponto fora dele chama-se P. Por P passa outro plano paralelo a A. Como são infinitas as retas que contêm P e pertencem ao plano que contém P, então são infinitas as retas paralelas ao plano A.
e) Falsa!
Apenas três pontos colineares determinam um único plano.
Gabarito: Letra D.
