Exercícios sobre Posições relativas
Verifique o posicionamento da reta r, dada pela equação 2x + y – 1 = 0 em relação à circunferência de equação x² + y² + 6x – 8y = 0.
Determinar as coordenadas do centro da circunferência é a medida do raio:
x² + y² + 6x – 8y = 0
x² + 6x + y² – 8y = 0
x² + 6x → completando o trinômio
x² + 6x + 9 = (x + 3)²
y² – 8y → completando o trinômio
y² – 8y + 16 = (y – 4)²
x² + 6x + y² – 8y = 0
x² + 6x + 9 + y² – 8y + 16 = 9 + 16
(x + 3)² + (y – 4)² = 25
A fórmula geral de uma equação da circunferência é dada por (x – a)² + (y – b)² = r², dessa forma:
Coordenadas do centro: (–3; 4)
Medida do raio: 5
Determinando a distância entre o centro e a reta
Reta r: 2x + y – 1 = 0
.gif)
Temos que a distância é menor que o raio, pois 1,3 < 5. Dessa forma, a reta é secante à circunferência.
Dada a reta s representada pela equação 2x – y + 1 = 0 e a circunferência de equação
x² + y² – 2x = 0, determine a posição relativa entre elas.
Vamos estabelecer um sistema entre as duas equações:
Reta: 2x – y + 1 = 0
Circunferência: x² + y² – 2x = 0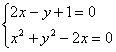
Resolvendo o sistema pelo método da substituição:
Isolando y na 1ª equação:
2x – y + 1 = 0
– y = –1 – 2x
y = 1 + 2x
Substituindo y na 2ª equação:
x² + (1 + 2x)² – 2x = 0
x² + 1 + 4x + 4x² – 2x = 0
5x² + 2x + 1 = 0
∆ = b² – 4ac
∆ = 2² – 4 * 5 * 1
∆ = 4 – 20
∆ = –16
Quando ∆ < 0, a equação não possui raízes. Dessa forma o sistema não possuirá soluções. Portanto, a reta é externa à circunferência.
Determine o valor de w sabendo que a reta de equação x – y + w = 0 é tangente à circunferência de equação x² + y² = 9.
Se a reta é tangente à circunferência, temos que a distância do centro até a reta possui a mesma medida do raio.
Em razão da equação x² + y² = 9, podemos dizer que o centro corresponde a (0; 0) e o raio igual a 3, pois x² + y² = 9 → (x + 0)² + (y + 0)² = 3².
Distância do centro (0; 0) à reta x – y + w = 0, onde a = 1, b = –1 e c = w:
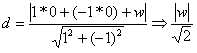
Calculando w de acordo com d = r:
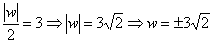
O valor de w é igual a + 3√2 ou –3√2.
(UFBA)
Determine o comprimento da corda determinada pela intersecção da reta r, de equação x + y – 1 = 0, com a circunferência de equação x² + y² + 2x + 2y – 3 = 0.
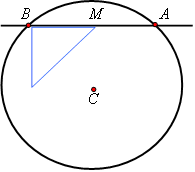
AB = medida da corda
CM = distância entre centro e reta
AM = metade da medida da corda → AB/2.
No triângulo AMC aplicaremos o teorema de Pitágoras, mas para isso precisaremos determinar a distância CM e o raio da circunferência, dado por CA.
Centro da circunferência
x² + y² + 2x + 2y – 3 = 0
x² + 2x + y² + 2y = 3
x² + 2x + 1 + y² + 2y + 1 = 3 + 1 + 1
(x + 1)² + (y + 1)² = 5
Centro (–1, –1) e raio = √5.
Reta: x + y – 1 = 0
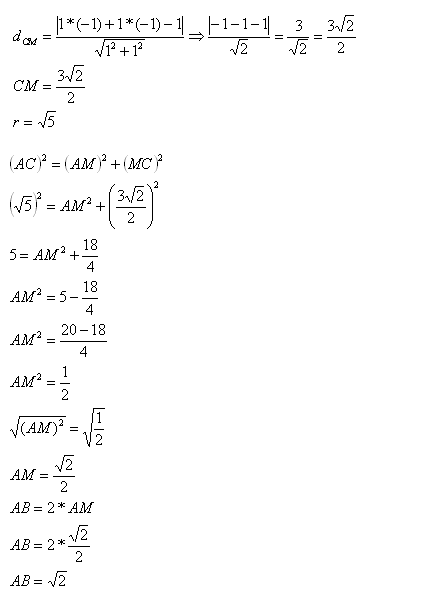
A medida da corda AB de acordo com a situação proposta é AB = √2.
(ITA-SP)
A distância entre os pontos de intersecção da reta com a circunferência x² + y² = 400 é:
a) 16√5
b) 4√5
c) 3√3
d) 4√3
e) 5√7
Resolver o sistema de equações:
.gif)
Simplificando a 1ª equação:
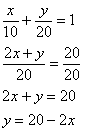
Substituindo x na 2ª equação:
x² + y² = 400
x² + (20 – 2x)² = 400
x² + 400 – 80x + 4x² ¬– 400 = 0
5x² – 80x = 0
5x * (x – 16) = 0
5x = 0
x’ = 0
x – 16 = 0
x’’ = 16
Para x = 0, temos:
y = 20 – 2x
y = 20 – 2*0
y = 20
(0; 20)
Para x = 16, temos:
y = 20 – 2x
y = 20 – 2 * 16
y = 20 – 32
y = – 12
(16; –12)
Os pontos de intersecção são (0; 20) e (16; –12).
Determinando a distância entre os pontos:
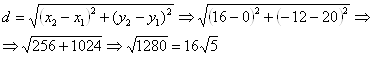
Resposta item a.
(UFRS)
O valor de k que transforma a equação x² + y² – 8x + 10y + k = 0 na equação de uma circunferência de raio 7 é:
a) –4
b) –8
c) 5
d 7
e) –5
x² + y² – 8x + 10y + k = 0
Encontrar a equação reduzida (completar os trinômios)
x² – 8x + y² + 10y = –k
x² – 8x + 4 + y² + 10y + 25 = – k + 4 + 25
(x – 4)² + (x + 5)² = –k + 41
Temos que o raio será dado por:
–k + 41 = 7²
–k = 49 – 41
–k = 8
k = 8
Resposta: alternativa b.
