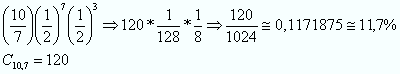Exercícios sobre Propriedades da Probabilidade
Teste os seus conhecimentos: Faça exercícios sobre Propriedades da Probabilidade e veja a resolução comentada.
Publicado por: Marcos Noé Pedro da SilvaQuestões
-
Questão 1
No lançamento de dois dados perfeitos, qual a probabilidade de que a soma dos resultados obtidos seja igual a 6?
Para que a soma seja 6, precisamos das seguintes faces: {(1,5), (2,4), (3,3), (4,2), (5,1)}. E considerando que o espaço amostral do lançamento de dois dados e representado pela multiplicação 6 * 6 = 36, temos a seguinte probabilidade:

A probabilidade é de 5/36, aproximadamente 13,88% de chance.
-
Questão 2
Considerando todos os divisores positivos do numeral 60, determine a probabilidade de escolhermos ao acaso, um número primo.
Divisores de 60: (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60). Temos um espaço amostral de 12 elementos, dos quais 3 são primos. Portanto, a probabilidade de escolhermos ao acaso, um número primo dentro dos divisores do número 60, será dada por:
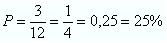
A probabilidade é de 25% de chance.
-
Questão 3
Em uma urna existem bolas enumeradas de 1 a 15. Qualquer uma delas possui a mesma chance de ser retirada. Determine a probabilidade de se retirar uma bola com número nas seguintes condições:
a) par
b) primo
c) par ou primo
d) par e primoEspaço amostral: (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)
a) No espaço amostral de 15 números, temos 7 números pares.
P = 7/15 = 0,466 = 46,6%b) Temos 6 números primos dentre o espaço amostral de 15 números.
P = 6/15 = 0,4 = 40%c)
Número par = 7 possibilidades entre 15
Número primo = 6 possibilidades entre 15
Par ∩ primo = 1P(par) + P(primo) – P (par ∩ primo)
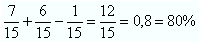
d) Dentro do intervalo dado, temos um único número que satisfaz a condição de ser par e primo ao mesmo tempo, que é o número 2. Portanto, temos a seguinte probabilidade:
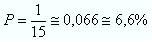
-
Questão 4
Um teste de múltipla escolha é composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Calcule a probabilidade de uma pessoa, marcando aleatoriamente as 12 questões, acertar metade das respostas.
As chances de acerto são 1 em 5, que corresponde a 0,2 ou 20%.
As chances de erro são 4 em 5, que corresponde a 08 ou 80%.Nesse caso, vamos utilizar a fórmula do método binomial:
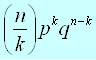
Vamos considerar acertos (p) e erros (q), então:
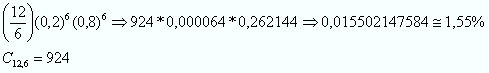
Ele possui 1,55% de chance de acertar metade das questões.
-
Questão 5
Uma moeda é lançada 10 vezes. Determine a probabilidade de sair “coroa” 7 vezes.
Chance de sair cara = 1/2
Chance de não sair cara (sair coroa) = 1/2