Exercícios sobre SAC: Sistema de Amortizações Constantes
Um empréstimo de R$ 60 000,00 deve ser devolvido de acordo com o sistema de amortizações constantes em 120 prestações mensais a taxa de juros de 1% ao mês. Construa a planilha referente as 5 primeiras prestações.
Vamos calcular o valor das amortizações constantes mensais, dividindo o valor do financiamento pelo número de prestações:
60000 : 120 = 500
Planilha
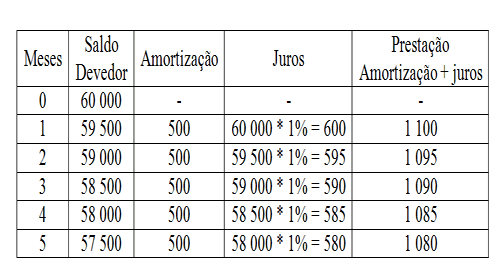
A planilha oferece o valor das 5 primeiras prestações do financiamento.
Um empréstimo de R$ 30 000,00 deve ser devolvido de acordo com o sistema de amortizações constantes em 60 prestações mensais a taxa de juros de 1% ao mês. Determine o valor da prestação de número 38 e o valor dos juros cobrados dessa prestação.
Ao analisarmos a planilha percebemos que a sequência de valores das prestações se assemelha ao comportamento de uma progressão aritmética decrescente. A razão dessa progressão pode ser calculada a partir da segunda prestação subtraindo um valor pelo seu antecessor. Observe:
Prestação 4 – Prestação 3 = 1 085 – 1 090 = –5
Prestação 5 – Prestação 4 = 1 080 – 1 085 = –5
A razão da progressão é uma constante negativa, devido a sua característica decrescente. Para determinarmos o valor da prestação de número 38 utilizaremos a prestação 1 (1º termo da progressão), a posição 38 (número de termos) e a razão decrescente. Veja:
an = a1 + (n – 1) * r
a38 = 1 100 + (38 – 1) * (–5)
a38 = 1 100 + (37) * (–5)
a38 = 1 100 + (–185)
a38 = 1 100 – 185
a38 = 915
No caso dos juros temos que a razão também é dada por –5. A primeira taxa de juros corresponde a R$ 600 e o número de termos igual a 38. Portanto:
a38 = 600 + (38 – 1) * (–5)
a38 = 600 + (–185)
a38 = 600 – 185
a38 = 415
A prestação de número 38 terá valor igual a R$ 915,00 e o valor dos juros cobrados na sua composição será de R$ 415,00.
(Concurso Receita Federal)
Um empréstimo no valor de R$ 40 000,00 foi concedido no regime de amortizações constantes e deverá ser quitado em 40 prestações mensais. Considerando a taxa de juros de 2% ao mês, determine o valor da amortização acumulada, dos juros, da prestação e do saldo devedor correspondente ao 21º mês.
Calculando a amortização mensal:
A = 40 000 / 40
A = 1 000
Construiremos a planilha referente aos 3 primeiros meses desse financiamento, no intuito de coletarmos dados para a resolução dos itens questionados.
.gif)
Amortização acumulada referente até a 21ª prestação
A21 = 1 000 * 21
A21 = 21 000
Juros
an = a1 + (n – 1) * r
a21 = 800 + (21 – 1) * (–20)
a21 = 800 + (20) * (–20)
a21 = 800 – 400
a21 = 400
Prestação
an = a1 + (n – 1) * r
a21 = 1 800 + (21 – 1) * (–20)
a21 = 1 800 + (20) * (–20)
a21 = 1 800 – 400
a21 = 1 400
Saldo Devedor
a21 = 40 000 + (20) * (–1000)
a21 = 40 000 – 20 000
a21 = 20 000
Em relação à 21ª prestação temos que a amortização acumulada corresponde a R$ 21 000, o valor dos juros cobrados será de R$ 400, a prestação terá valor igual a R$ 1 400 e o saldo devedor R$ 20 000.
(Concurso Controlador da Arrecadação Fiscal)
Um empréstimo no valor de R$ 2 000 000 é concedido à taxa de juros compostos de 10% ao ano, a ser reembolsado em 5 anos de acordo com o SAC. Determine o valor total do financiamento após a quitação através da construção da planilha de dados dessa operação financeira.
.gif)
O valor final do financiamento corresponde o total de R$ 2 600 000.
