Exercícios sobre a semelhança entre triângulos
Existem alguns procedimentos que podem ser usados para descobrir se dois triângulos são semelhantes sem ter de analisar a proporcionalidade de todos os lados e, ao mesmo tempo, as medidas de todos os ângulos desses triângulos. A respeito desses casos, assinale a alternativa correta:
a) Para que dois triângulos sejam semelhantes, basta que eles tenham três ângulos correspondentes congruentes.
b) Para que dois triângulos sejam semelhantes, basta que eles tenham dois lados proporcionais e um ângulo congruente, em qualquer ordem.
c) Para que dois triângulos sejam congruentes, basta que eles tenham os três lados correspondentes com medidas proporcionais.
d) Dois triângulos que possuem dois lados correspondentes proporcionais não serão semelhantes em qualquer hipótese.
e) Dois triângulos que possuem apenas dois ângulos correspondentes congruentes não podem ser considerados semelhantes.
a) Incorreta!
São necessários apenas dois ângulos correspondentes congruentes para que dois triângulos sejam semelhantes.
b) Incorreta!
Os triângulos precisam ter dois lados correspondentes proporcionais e o ângulo que fica entre esses dois lados precisa ser congruente para que os dois triângulos sejam semelhantes. Assim, não é em qualquer ordem.
c) Correta!
d) Incorreta!
Para que esses triângulos sejam semelhantes, basta que o ângulo entre esses dois lados seja congruente.
e) Incorreta!
Esse é justamente um dos casos de semelhança de triângulos.
Gabarito: Letra C.
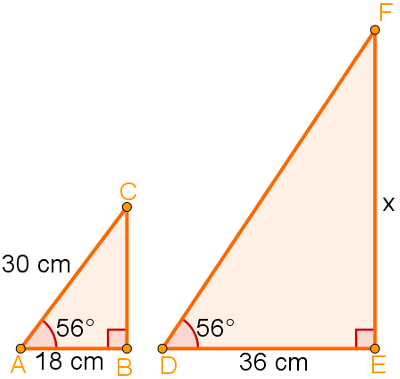
Qual o valor de x nos triângulos a seguir?
a) 48 cm
b) 49 cm
c) 50 cm
d) 24 cm
e) 20 cm
Observe que os dois triângulos são semelhantes pelo caso AA. Entretanto, x é a medida do lado EF do triângulo maior, que, por sua vez, é correspondente ao lado CB do triângulo menor. Para descobrir a medida desse lado, podemos usar o teorema de Pitágoras:
302 = 182 + y2
900 = 324 + y2
y2 = 900 – 324
y2 = 576
y = √576
y = 24 cm
Como os lados dos triângulos são proporcionais, para descobrir a medida de x, basta usar a proporção entre os lados:
18 = 24
36 x
18x = 36·24
18x = 864
x = 864
18
x = 48 cm.
Gabarito: Letra A.
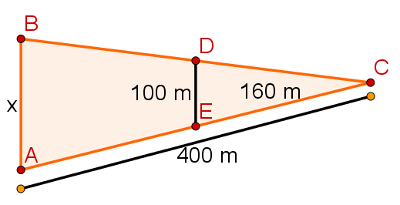
Na imagem a seguir, é possível perceber dois triângulos que compartilham parte de dois lados. Sabendo que os segmentos BA e DE são paralelos, qual a medida de x?
a) 210 m
b) 220 m
c) 230 m
d) 240 m
e) 250 m
Quando um triângulo é cortado por um segmento de reta paralelo a um de seus lados, esse segmento forma um segundo triângulo menor e semelhante ao primeiro. É o caso desse exercício. Para resolver essa questão, usaremos apenas a proporção:
400 = 160
x 100
160x = 400·100
160x = 40000
x = 40000
160
x = 250 m
Gabarito: Letra E.
Para descobrir a altura de um prédio, Luiz mediu a sombra do edifício e, em seguida, mediu sua própria sombra. A sombra do prédio media 7 metros, e a de Luiz, que tem 1,6 metros de altura, media 0,2 metros. Qual a altura desse prédio?
a) 50 metros
b) 56 metros
c) 60 metros
d) 66 metros
e) 70 metros
Em problemas desse tipo, a sombra e a altura do prédio, assim como a sombra e a altura da pessoa – ou qualquer outro objeto usado para comparação –, formam triângulos retângulos, que são semelhantes, pois a sombra e a altura dos objetos são lados proporcionais e, entre eles, há um ângulo de 90°. Assim, para resolver esse problema, basta calcular a proporção entre altura e comprimento da sombra:
7 = 0,2
x 1,6
0,2x = 7·1,6
0,2x = 11,2
x = 11,2
0,2
x = 56 metros
Gabarito: Letra B.
