Exercícios sobre semirreta, semiplano e semiespaço
A respeito da definição e das diferenças entre as semirretas e as retas, assinale a alternativa correta.
a) Uma semirreta determina o espaço unidimensional, no qual podem ser construídas outras figuras geométricas como a reta, o segmento de reta e o ponto.
b) Uma semirreta é um conjunto de pontos que pode ser compreendido como parte de uma reta, a qual possui começo e fim.
c) Uma semirreta é diferente de uma reta porque pode fazer curvas e a reta, não.
d) Uma semirreta é resultado de um “corte” feito em uma reta. Sendo assim, as semirretas têm um ponto inicial, mas não possuem um ponto final.
e) É impossível construir um segmento de reta dentro de uma semirreta.
As semirretas são resultados de um “corte” feito sobre uma reta. Elas possuem um ponto inicial, mas não apresentam um ponto final. Assim sendo, as semirretas não podem ser consideradas o espaço unidimensional. Esse papel é da reta, que é infinita para ambas as direções. Com relação à construção de segmentos de reta, é perfeitamente possível construí-los na semirreta. Dessa maneira, a alternativa correta é a letra D.
Gabarito: Alternativa D.
A respeito da definição e da relação dos semiplanos com o plano, assinale a alternativa correta.
a) Um semiplano é uma das duas partes formadas a partir de um corte feito em um plano por meio de uma reta.
b) Um semiplano possui dimensão igual a 0,5, pois é igual à metade de um plano.
c) Um semiplano é o espaço bidimensional no qual todas as formas geométricas planas podem ser construídas.
d) O plano e o semiplano são figuras geométricas idênticas.
e) Um semiplano é um plano que possui ponto inicial, mas não possui ponto final.
Um semiplano é o resultado do “corte” de um plano por meio de uma reta. Sendo assim, a alternativa correta é a letra A. O semiplano continua com dimensão igual a 2, assim como o plano é o espaço bidimensional. O semiplano pode ser considerado uma figura geométrica infinita construída no espaço bidimensional, por isso, semiplano e plano são objetos distintos. Como o semiplano é resultado de um “corte” feito por uma reta, não é possível dizer que ele tenha um “ponto inicial” como as semirretas.
Gabarito: Alternativa A.
A respeito dos semiespaços e de sua definição, assinale a alternativa correta.
a) Um semiespaço e um semiplano possuem o mesmo número de dimensões.
b) Um semiespaço é o espaço de dimensão 3, no qual todos os sólidos geométricos podem ser construídos.
c) Os semiespaços possuem metade do tamanho do espaço, portanto, seu número de dimensões também é igual à metade do número de dimensões do espaço.
d) O semiespaço e o espaço são infinitos para todas as direções.
e) Um corte feito por um semiplano em um espaço não pode gerar um semiespaço.
Um semiespaço é o resultado do “corte” feito em um espaço por um plano. Sendo assim, o número de dimensões do semiespaço e do espaço é o mesmo. Além disso, o espaço tridimensional é o que chamamos de espaço; o semiespaço é limitado por um plano em uma de suas direções. Portanto, a alternativa correta é a letra E.
Gabarito: Alternativa E.
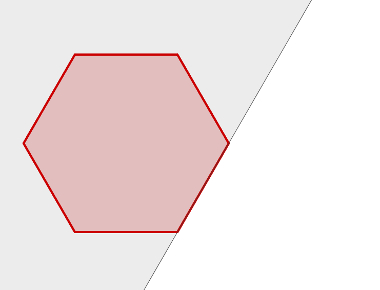
Analise a seguinte imagem que possui um polígono dentro de um semiplano e assinale a alternativa correta.
a) Se todos os lados do polígono determinam um semiplano que contém todo o polígono, então, ele é convexo.
b) O semiplano é a parte vermelha da imagem.
c) O polígono é regular todas as vezes que um de seus lados coincide com o limite de um semiplano.
d) Não há nenhuma propriedade que ligue o polígono ao semiplano.
e) O polígono e o semiplano não podem possuir o mesmo número de dimensões, uma vez que o polígono é mais limitado que o semiplano.
Sempre que todos os lados do polígono determinarem um semiplano contendo todo o polígono, esse polígono será convexo. Portanto, o gabarito da questão é a alternativa A.
Na imagem, o semiplano é toda a parte limitada pela reta que passa pelo lado do polígono. Além disso, não há ligação entre polígonos regulares e limites de semiplanos. A alternativa D está errada porque a alternativa A apresenta uma propriedade que liga essas duas figuras; a alternativa E está errada porque ambas as figuras são bidimensionais.
Gabarito: Alternativa A.
