Exercícios sobre sistemas lineares
Durante uma visita à padaria, Kárita comprou 2 pedaços de bolo de cenoura e uma dose de café, pagando, ao todo, R$ 3,50. Sua irmã, Karla, comprou 1 pedaço de bolo de cenoura e 2 doses de café, pagando um total de R$ 2,50. Analisando essa situação, se uma pessoa comprar 1 pedaço de bolo de cenoura e 1 café, o valor pago por ela será de:
A) R$ 1,00
B) R$ 1,50
C) R$ 1,75
D) R$ 2,00
E) R$ 2,25
Alternativa D
Para montar o sistema de equações, temos:
x → valor do pedaço do bolo de cenoura
y → valor da dose de café
Então, calcula-se:
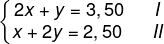
Pelo método da substituição, isolando y na equação I, obtém-se o seguinte:
y = 3,5 – 2x
Substituindo na equação II:
x + 2 (3,5 – 2x) = 2,5
x + 7 – 4x = 2,5
– 3x = 2,5 – 7
– 3x = – 4,5
x = – 4,5 : ( – 3)
x = 1,5
Sabendo que x = 1,5, substituímos o valor na equação I:
2x + y = 3,50
2 · 1,5 + y = 3,50
3 + y = 3,50
y = 3,50 – 3
y = 0,5
Sendo assim, o preço de um pedaço de bolo mais uma dose de café é de 1,5 + 0,5 = 2, ou seja, R$ 2,00.
Em um estacionamento, há motos e carros, em um total de 25 veículos. Sabendo há 74 rodas nesse estacionamento, podemos afirmar que
A) há 1 carro a mais que a quantidade de motos.
B) há 2 carros a mais que a quantidade de motos.
C) há 1 moto a mais que a quantidade de carros.
D) há 2 motos a mais que a quantidade de carros.
Alternativa C
Para montar o sistema, temos:
x → quantidade de carros
y → quantidade de motos
Então, calcula-se:
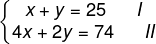
Isolando y na equação I:
y = 25 – x
Substituindo na equação II:
4x + 2 (25 – x) = 74
4x + 50 – 2x = 74
2x = 74 – 50
2x = 24
x = 24 : 2
x = 12 → Há 12 carros.
Como há um total de 25 veículos, então 25 – 12 = 13. Logo, há 13 motos.
Podemos afirmar, portanto, que há 1 moto a mais que a quantidade de carros.
Matheus tem um total de R$ 115,00 em notas de R$ 5,00 e de R$ 20,00. Considerando que ele possui um total de 11 cédulas, a quantidade de notas de R$ 5,00 que ele possui a mais que as de R$ 20,00 é igual a:
A) 2
B) 3
C) 4
D) 5
E) 7
Alternativa B
Para montar o sistema, temos:
x → quantidade de notas de 5,00
y → quantidade de notas de 20,00
Então, calcula-se:
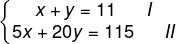
Isolando o x na equação I:
x = 11 – y
Substituindo na equação II:
5 (11 – y) + 20y = 115
55 – 5y + 20y = 115
15y = 115 – 55
15y = 60
y = 60 : 15
y = 4
Sabendo que há 4 notas de 20 reais:
x + y = 11
x + 4 = 11
x = 11 – 4
x = 7
Logo, 7 – 4 = 3, então há 3 notas de R$ 5,00 a mais que notas de R$ 20,00.
Sabe-se x e y são as incógnitas do seguinte sistema linear:
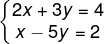
O valor do produto entre x e y é:
A) 0
B) 1
C) 2
D) 4
E) 5
Alternativa A
I → 2x + 3y = 4
II → x – 5y = 2
Isolaremos a variável x na equação II:
x = 2 – 5y
Agora, substituiremos x na equação I:
2 (2 – 5y) + 3y = 4
4 – 10y + 3y = 4
4 – 7y = 4
– 7y = 4 – 4
– 7y = 0
y = 0 : ( – 7)
y = 0
Sabendo que y = 0, obtemos:
x – 5y = 2
x – 5 · 0 = 2
x – 0 = 2
x = 2
Dessa forma, o produto é de 2 · 0 = 0.
Em um clube, há dois tipos de público, os sócios e os não sócios. Durante o evento da virada de ano, o clube decidiu fazer uma festa em que os sócios pagariam R$ 50,00 para participar e os não sócios pagariam R$ 120,00. Sabendo que no evento havia um total de 300 pessoas e que foram arrecadados R$ 22.700,00, o número de sócios e não sócios que foram à festa é de, respectivamente,
A) 210 e 90.
B) 190 e 110.
C) 180 e 120.
D) 150 e 150.
E) 200 e 100.
Alternativa B
Sendo x a quantidade de sócios e y a quantidade de não sócios, de acordo com as informações dadas, podemos montar o seguinte sistema de equações:
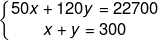
Na segunda equação, isolaremos x:
x + y = 300
x = 300 – y
Agora, substituiremos na primeira equação o valor de x:
50 (300 – y) + 120 y = 22700
15000 – 50y + 120y = 22700
70y = 22700 – 15000
70y = 7700
y = 7700 : 70
y = 110
Considerando que havia 110 não sócios, o número de sócios é igual a 300 – 110 = 190.
Resolvendo o sistema linear a seguir
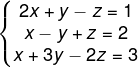
podemos afirmar que o valor de z que satisfaz esse sistema é igual a:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa E
Utilizando a regra de Cramer, devemos calcular o determinante da matriz incompleta.
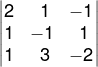
D = 2⋅( − 1)⋅( − 2) + 1 ⋅ 1 ⋅ 1 + ( − 1) ⋅ 1 ⋅ 3 − 1 ⋅ ( − 1) ⋅ ( − 1) −3 ⋅ 1 ⋅ 2 − ( − 2) ⋅ 1 ⋅ 1 = − 3
Na matriz incompleta, substituiremos a terceira coluna pelos termos independentes e calcularemos o determinante Dz.
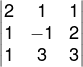
Dz = 2 ⋅ ( − 1) ⋅ 3 + 1 ⋅ 2 ⋅ 1 + 1 ⋅ 1 ⋅ 3 − 1 ⋅ ( − 1) ⋅ 1 − 3 ⋅ 2 ⋅ 2 − 3 ⋅ 1 ⋅ 1 = − 15
Agora é possível encontrar o valor de z, dividindo Dz por D:
z = – 15 : ( – 3) = 5
São considerados métodos de resolução de sistemas lineares, exceto:
A) Regra de Cramer
B) Escalonamento
C) Método da adição
D) Método da substituição
E) Balanceamento
Alternativa E
Das alternativas propostas, somente o balanceamento não é um método utilizado para resolver sistemas lineares.
Os bichos de pelúcia Pluto e Mickey pesam juntos 52 kg. Sabendo que a diferença entre os pesos de Pluto e Mickey é de 4 kg, então Mickey pesa
A) 28 kg.
B) 27 kg.
C) 26 kg.
D) 25 kg.
E) 24 kg.
Alternativa E
P → peso de Pluto
M → peso de Mickey
Com as variáveis, montamos o seguinte sistema:
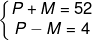
Somando as equações, temos:
2P + 0M = 56
2P = 56
P = 56 : 2
P = 28
Agora que sabemos o peso de Pluto, encontraremos o peso de Mickey:
P + M = 52
28 + M = 52
M = 52 – 28
M = 24 kg
(Enem 2018) Durante uma festa de colégio, um grupo de alunos organizou uma rifa. Oitenta alunos faltaram à festa e não participaram da rifa. Entre os que compareceram, alguns compraram 3 bilhetes, 45 compraram 2 bilhetes e muitos compraram apenas 1. O total de alunos que comprou 1 único bilhete era 20% do número total de bilhetes vendidos, e o total de bilhetes vendidos excedeu em 33 o número total de alunos do colégio.
Quantos alunos compraram somente 1 bilhete?
A) 34
B) 42
C) 47
D) 48
E) 79
Alternativa D
Sabemos que 80 alunos não compraram bilhetes e que 45 alunos compraram 2 bilhetes. Sendo x o número de alunos compraram 1 bilhete e y o número de alunos que compraram 3 bilhetes, o total de bilhetes vendidos é dado pela seguinte equação:
x + 2 · 45 + 3y
x + 90 + 3y
Já o total de estudantes pode ser representado pela seguinte equação:
x + y + 80 + 45
x + y + 125
Sabemos que o número de ingressos vendidos excedeu em 33 o número total de alunos, então temos:
x + 90 + 3y = 33 + 125 + x + y
x – x + 3y – y = 33 + 125 – 90
2y = 68
y = 34
Segundo o enunciado, 20% dos bilhetes é igual à quantidade de alunos que compraram somente um bilhete, portanto:
x = 0,2 · total de alunos
x = 0,2 (x + 90 + 3y)
x = 0,20 (x + 90 + 3 · 34)
x = 0,2 (x + 192)
x = 0,2x + 38,4
x – 0,2x = 38,4
0,8x = 38,4
x = 38,4 : 0,8
x = 48
(MS Concursos) O sistema de equações:
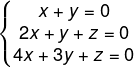
A) não tem solução.
B) admite apenas uma solução trivial.
C) admite infinitas soluções.
D) admite apenas soluções não triviais.
Alternativa C
Na primeira equação, temos:
x + y = 0
x = – y
Substituindo x por – y na segunda equação, calcula-se:
2x + y + z = 0
2 ( – y) + y + z = 0
– 2y + y + z = 0
– y + z = 0
z = y
Por fim, substituindo x por – y e z por y na terceira equação, obtém-se o seguinte:
4x + 3y + z = 0
4 ( – y) + 3y + y = 0
– 4y + 3y + y = 0
0 = 0
Logo, temos como soluções do sistema qualquer par ordenado, sendo y = y, x = – y e z = y. Assim, esse sistema possui infinitas soluções.
(Saeb 2011) Um teste é composto por 20 questões classificadas em verdadeiras ou falsas. O número de questões verdadeiras supera o número de questões falsas em 4 unidades. Sendo x o número de questões verdadeiras e y o número de questões falsas, o sistema associado a esse problema é:
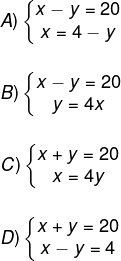
Alternativa D
Sendo x o número de questões verdadeiras e y o número de questões falsas, consideramos que a soma entre eles é igual a 20, ou seja:
x + y = 20
Além disso, sabemos que há 4 questões verdadeiras a mais que questões falsas, então a diferença entre o número de questões verdadeiras e o número de questões falsas é 4. Ou seja:
x – y = 4
A alternativa que contém o sistema com essas duas equações é a alternativa D.
(IFPE) Com a proximidade do final do ano, uma papelaria quis antecipar as promoções de material didático para o ano letivo de 2012. Foram colocados em promoção caneta, caderno e lápis. As três ofertas eram:
1ª) 5 canetas, 4 cadernos e 10 lápis por R$ 62,00;
2ª) 3 canetas, 5 cadernos e 3 lápis por R$ 66,00;
3ª) 2 canetas, 3 cadernos e 7 lápis por R$ 44,00.
Para comparar os preços unitários dessa papelaria com outras do comércio, o Sr. Ricardo calculou os preços de uma caneta, um caderno e um lápis. A soma desses preços é
A) R$ 20,00.
B) R$ 18,00.
C) R$ 16,00.
D) R$ 14,00.
E) R$ 12,00.
Alternativa D
Montando o sistema, temos:
x → preço da caneta
y → preço do caderno
z → preço do lápis
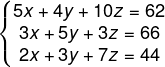
Agora, utilizando a regra de Cramer, calcularemos D, Dx, Dy e Dz. Montando os determinantes:
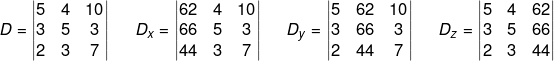
D = 5 ⋅ 5 ⋅ 7 + 4 ⋅ 3 ⋅ 2 + 10 ⋅ 3 ⋅ 3 − 2 ⋅ 5 ⋅ 10 − 3 ⋅ 3 ⋅ 5 − 7 ⋅ 3 ⋅ 4 = 60
Dx = 62 ⋅ 5 ⋅ 7 + 4 ⋅ 3 ⋅ 44 + 10 ⋅ 66 ⋅ 3 − 44 ⋅ 5 ⋅ 10 − 3 ⋅ 3 ⋅ 62 − 7⋅ 66 ⋅ 4 = 72
Dy = 5 ⋅ 66 ⋅ 7 + 62 ⋅ 3 ⋅ 2 + 10 ⋅ 3 ⋅ 44 − 2 ⋅ 66 ⋅ 10 − 44 ⋅ 3 ⋅ 5 − 7 ⋅ 3 ⋅ 62 = 720
Dz = 5 ⋅ 5 ⋅ 44 + 4 ⋅ 66 ⋅ 2 + 62 ⋅ 3 ⋅ 3 − 2 ⋅ 5 ⋅ 62 − 3 ⋅ 66 ⋅ 5 − 44 ⋅ 3 ⋅ 4 = 48
Dessa forma, obtém-se:
x = Dx : D = 72 : 60 = 1,20
y = Dy : D = 720: 60 = 12,00
z = Dz : D = 48 : 60 = 0,80
Portando, a soma do preço P de uma caneta mais um caderno mais um lápis é igual a:
P = 1,20 + 12,00 + 0,80 = 14,00
