Exercícios sobre sólidos geométricos
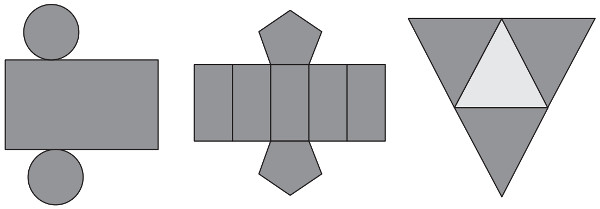
(Enem 2012) Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
a) Cilindro, prisma de base pentagonal e pirâmide.
b) Cone, prisma de base pentagonal e pirâmide.
c) Cone, tronco de pirâmide e pirâmide.
d) Cilindro, tronco de pirâmide e prisma.
e) Cilindro, prisma e tronco de cone.
Alternativa A
Um cilindro é um sólido geométrico que possui duas bases circulares e que a planificação de sua superfície lateral é um paralelogramo. A primeira imagem, portanto, é a planificação de um cilindro.
Um prisma é um sólido geométrico que possui duas bases poligonais congruentes e todas as suas faces laterais são paralelogramos. Quando uma das bases do prisma é um pentágono, ele é chamado de “prisma de base pentagonal” e possui como faces laterais cinco paralelogramos, exatamente como a segunda figura.
Uma pirâmide é um sólido geométrico formado por uma base poligonal e todas as suas faces laterais são triângulos. Na terceira imagem, a base é um triângulo e as faces laterais também. Todos eles são congruentes, portanto, essa imagem diz respeito à planificação de uma pirâmide.
Portanto, a resposta correta é: cilindro, prisma de base pentagonal e pirâmide.
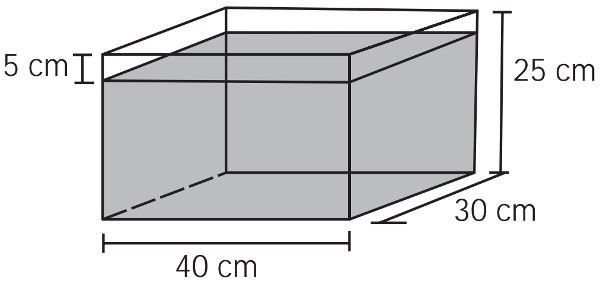
(Enem 2012) Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento como mostrado na figura.
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2400 cm3?
a) O nível subiria 0,2 cm, fazendo a água ficar com 20,2 cm de altura.
b) O nível subiria 1 cm, fazendo a água ficar com 21 cm de altura.
c) O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura.
d) O nível subiria 8 cm, fazendo a água transbordar.
e) O nível subiria 20 cm, fazendo a água transbordar.
Alternativa C
Suponha que o objeto possui largura e comprimento exatamente iguais aos do tanque. Sabendo que o volume desse objeto é igual a 2400 cm3, sua altura será justamente a quantidade de centímetros que a água subiria. Para encontrar a altura desse objeto, basta usar a fórmula do volume do paralelepípedo:
V = Ab·h
Ab é a área da base, e h é a altura. A área da base desse objeto, supondo que ele possui mesmo comprimento e largura que o tanque, é:
Ab = 30·40
Ab = 1200 cm2
Substituindo esse valor e o volume do objeto na fórmula do volume, teremos:
V = Ab·h
2400 = 1200·h
2400 = h
1200
2 = h
h = 2
Como as medidas são dadas em centímetros, a altura do objeto será igual a 2 cm, ou seja, o nível da água subirá 2 cm, alcançando a altura de 22 cm.
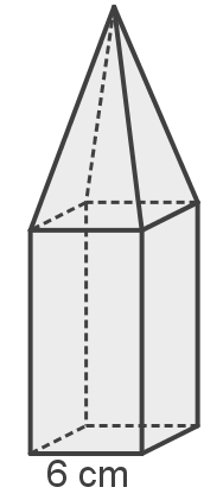
Uma pirâmide reta de base quadrada foi soldada sobre um prisma reto de bases congruentes à base da pirâmide, formando um sólido geométrico parecido com o da figura.
Sabendo que a aresta da base do prisma mede 6 cm e que sua altura e a altura da pirâmide medem o dobro da aresta da base do prisma, qual o volume do sólido geométrico formado nessa construção?
a) 144 cm3
b) 256 cm3
c) 288 cm3
d) 432 cm3
e) 576 cm3
Alternativa E
O volume desse sólido geométrico é dado pela soma do volume da pirâmide (V1) e do volumo do prisma (V2). Em outras palavras, o volume total (V) é dado por:
V = V1 + V2
Todas as arestas da base do prisma medem 6 cm, pois sua base é quadrada. Além disso, sua altura mede o dobro da aresta da base, portanto, 12 cm. O mesmo vale para a pirâmide: arestas da base medem 6 cm, e a altura mede 12 cm. Isso ocorre porque as bases dos dois sólidos são congruentes.
O volume de uma pirâmide qualquer é determinado por:
V = Ab·h
3
Como a base da pirâmide é quadrada e possui aresta de 6 cm, teremos:
Ab = l2
Ab = 62
Ab = 36
O volume dessa pirâmide será:
V1 = Ab·h
3
V1 = 36·12
3
V1 = 432
3
V1 = 144 cm3
Como as bases do prisma e da pirâmide são congruentes, suas áreas são iguais. A fórmula do volume do prisma é:
V2 = Ab·h
V2 = 36·12
V2 = 432 cm3
Para finalizar o exercício, basta calcular a área total do sólido geométrico:
V = V1 + V2
V = 144 + 432
V = 576 cm3
Por não conseguir medir a altura de um cone, um trabalhador mediu sua geratriz (distância entre o vértice do cone e a borda de sua base) e encontrou 25 cm de comprimento. Mediu também o diâmetro desse mesmo cone, encontrando 40 cm de comprimento. Qual é o volume do cone medido por esse trabalhador? (Considere π = 3)
a) 6000 cm3
b) 7000 cm3
c) 8000 cm3
d) 9000 cm3
e) 9500 cm3
Alternativa A
A fórmula usada para determinar o volume do cone é:
V = π.r2.h
3
O r é o raio do cone, e h, a sua altura. O raio desse cone é metade do diâmetro de sua base, pois a base de um cone é um círculo, e o diâmetro é igual a duas vezes o raio. Dessa maneira, o raio desse cone mede 40:2 = 20 cm.
Já a altura do cone é dada pela seguinte expressão:
g2 = r2 + h2
O g é a geratriz, r é o raio, e h é a altura. Substituindo os valores dados, teremos:
g2 = r2 + h2
252 = 202 + h2
625 = 400 + h2
625 – 400 = h2
225 = h2
√225 = √(h2)
15 = h
h = 15 cm
Tendo encontrado a medida da altura e já de posse da medida do raio do cone, podemos substituí-los na fórmula do volume:
V = π.r2.h
3
V = 3·202·15
3
V = 3·400·15
3
V = 3·6000
3
V = 6000 cm3
