Exercícios sobre Teorema de Laplace
Calcule o Determinante:
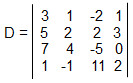
Vamos escolher a linha 3 para calcular o cofator, de acordo com o teorema de Lapalce, temos:
D= 7 . A31 + 4 . A32 + (-5). A33 + 0. A34
Faremos o cálculo dos determinantes individuais, note que obtemos uma matriz de ordem 3, pois retiramos a linha e a coluna do fator A31, somamos a posição: linha mais coluna : A 3 +1 = 4
.jpg)
A31 = 1. ( 42 - 33)
A31 = 1. 9
A31 = 9
Faremos o mesmo processo com os demais:
A32 = (-1)5. 
= 20
A33 = (-1)6 = 
= 7
D = 7. 9 + 4. 20 + (-5). 7 + 0
D = 108
Qual o valor de:
A escolha da linha ou coluna para calcular o cofator é aleatória, mas para facilitar escolhemos aquela que tiver maior número de 0, assim teremos que fazer menos cálculos. Então, 2° coluna:
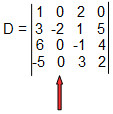
Utilizando o teorema de Laplace, temos:
D= 0. A12 + (-2) . A22 + 0 . A32 + 0. A42
D = (-2) . A22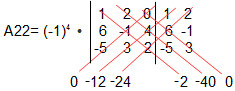
D = (-2) . (-78)
D = 156
Qual o valor do determinante?
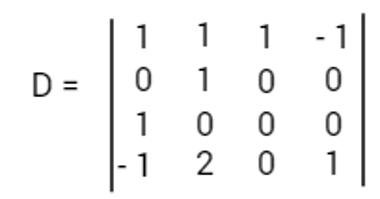
a) 1
b) 2
c) 0
d)-1
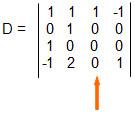3° coluna
Utilizando o teorema de Laplace:
D = 1. A13 + 0. A23 + 0 . A33 + 0. A43
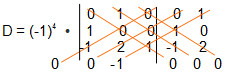
D = 1. (-1)
D = -1
Letra d.
O cofator do elemento A22 da matriz A = 
é:
a) 1
b) 2
c) 4
d) - 3
Para determinar o cofator, vamos fazer o determinante da matriz sem a linha e a coluna que esse elemento se encontra:
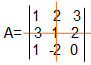
Assim, obtemos a seguinte matriz de ordem 2, Veja:
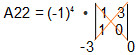
A22= - 3
Letra d.
