Exercícios sobre trapézio
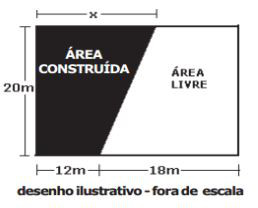
(EsPCEx) As regras que normatizam as construções em um condomínio definem que a área construída não deve ser inferior a 40% da área do lote e nem superior a 60% desta. O proprietário de um lote retangular pretende construir um imóvel de formato trapezoidal, conforme indicado na figura.
Para respeitar as normas acima definidas, assinale o intervalo que contém todos os possíveis valores de x.
a) [6, 10]
b) [8, 14]
c) [10, 18]
d) [16, 24]
e) [12, 24]
Inicialmente devemos calcular a área total do lote, que possui 20 m de altura e 30 m de comprimento (base). Como o lote é retangular, utilizaremos a fórmula do calculo de área:
Área = base . Altura
A = b x h
A = 20 m . 30 m
A = 600 m2
Agora vamos calcular o que corresponde à área construída de 40% e de 60%.
40% . 600 = 40 . 600 = 240 m2
100
60% . 600 = 60 . 600 = 360 m2
100
Como já sabemos as porcentagens, devemos calcular a área construída, que será dada pela função da área do trapézio. Essa função baseia-se na fórmula para o cálculo da área do trapézio e é dada por:
Função da área do trapézio = altura . (Base maior + base menor)
2
f(x) = h . (B + b)
2
f(x) = 20 . ( x + 12)
2
f(x) = 20x + 240
2
f(x) = 10x + 120
Vamos agora determinar o intervalo:
240 < 10x + 120 < 360
240 – 120 < 10x < 360 – 120
120 < 10x < 240
120 < x < 240
10 10
12 < x < 24
Logo, o intervalo é de [12, 24]. A alternativa correta é a letra e.
(PUC-SP) Um tanque de uso industrial tem a forma de um prisma cuja base é um trapézio isósceles. Na figura a seguir, são dadas as dimensões do prisma em metros. O volume desse tanque em metros cúbicos é?
.jpg "Tanque industrial no formato trapezoide")
a) 50
b) 60
c) 80
d) 100
e) 120
Inicialmente devemos calcular a medida de a. Ao observar a imagem do trapézio, visualizamos que a sua parte superior é um retângulo. Nessa forma geométrica, os lados opostos são paralelos e possuem a mesma medida. Então, um lado mede 9 e o outro mede (a + 2 + a).
Vamos determinar a medida de a:
a + 2 + a = 8
2a = 8 -2
a = 8 – 2 = 3 → a é o cateto do triângulo retângulo.
2
Agora vamos calcular a altura h utilizando o teorema de Pitágoras:
52 =h2 + a2
25 = h2 + 32
25 = h2 + 9
- h2 = 9 – 25
- h2 = - 16 . (-1)
h2 = 16 → efetue a raiz dos dois lados
h = 4
Com os valores obtidos, podemos calcular a área da base do prisma, que possui o formato de trapézio.
Área = altura . ( Base maior + base menor)
2
A = h . (B + b)
2
A = 4 . (8 + 2)
2
A = 4 . (10)
2
A = 40
2
A = 20
Podemos agora encontrar o volume do prisma, que é dado pelo produto da área da base do prisma por 5, que é a sua altura.
V= 20 . 5
V= 100
A alternativa correta para essa questão é a letra d.
Calcule a área do trapézio retângulo e isósceles abaixo:
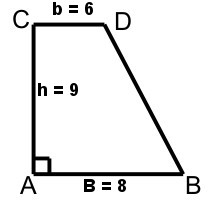
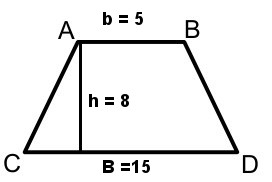
Área do trapézio retângulo
Área = altura . (Base maior + base menor)
2
A = h . (B + b)
2
A = 9 . ( 8 + 6)
2
A = 9 . 14
2
A = 126
2
A = 63
Área do trapézio isósceles
Área = altura . (Base maior + base menor)
2
A = h . (B + b)
2
A = 8 . ( 15 + 5)
2
A = 8 . 20
2
A = 160
2
A = 80
Calcule a área do trapézio escaleno abaixo:
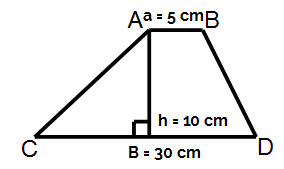
Área = altura . (Base maior + base menor)
2
A = h . ( B + b)
2
A = 10 . (5 + 30)
2
A = 10 . (35)
2
A = 350
2
A = 175 cm2
A área do trapézio escaleno é de 175 cm².
