Exercícios sobre triângulo escaleno
Esta lista contém exercícios sobre triângulos escalenos, com questões envolvendo área, perímetro e as principais características desse tipo de triângulo.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Ao realizar a classificação de triângulos, um triângulo será classificado como escaleno se:
A) ele possuir todos os lados congruentes.
B) ele possuir dois lados congruentes e um lado não congruente.
C) ele possuir todos os ângulos agudos.
D) ele possuir todos os lados com medidas distintas.
E) ele possuir área e perímetro iguais.
Alternativa D.
O triângulo é escaleno quando as medidas dos lados são todas distintas.
-
Questão 2
Uma reserva florestal possui formato triangular com lados medindo 9 km, 14 km e 7 km. Podemos afirmar que a área dessa reserva florestal é de aproximadamente:
A) 27 km².
B) 25 km².
C) 22 km².
D) 20 km².
E) 18 km².
Alternativa A.
Utilizando a fórmula de Heron, calcularemos primeiro o semiperímetro:
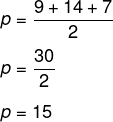
Conhecendo o valor de p, encontraremos o valor da área:
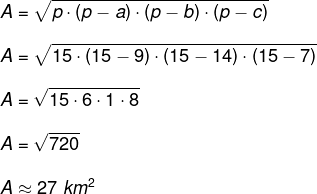
-
Questão 3
(Contemax) Nas segundas, quartas e sextas, Paulo faz o seguinte caminho: Casa → Escola → Fábrica → Casa. Nas terças e quintas ele faz o seguinte trajeto: Casa → Escola → Fábrica → Escola → Casa.
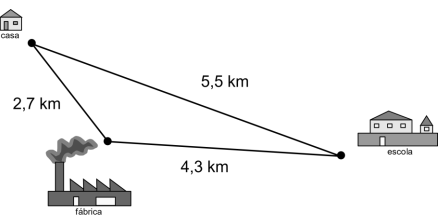
A distância percorrida por Paulo de segunda a sexta é:
A) 76,7 km.
B) 62,5 km.
C) 98,0 km.
D) 82,0 km.
E) 85,3 km.
lternativa A.
Analisando o percurso feito por ele de segunda, quarta e sexta, basta somar as distâncias:
Casa → Escola → Fábrica → Casa
5,5 + 4,3 + 2,7 = 12,5
Como ele faz esse percurso 3 vezes na semana, então 12,5 · 3 = 37,5.
Agora vamos realizar a soma do percurso feito na terça e quinta:
Casa → Escola → Fábrica → Escola → Casa.
5,5 + 4,3 + 4,3 + 5,5 = 19,6
Como ele faz esse percurso duas vezes na semana, temos que 19,6 · 2 = 39,2.
Agora basta realizar a soma: 37,5 + 39,2 = 76,7.
-
Questão 4
Um triângulo escaleno possui ângulos diretamente proporcionais aos números 10, 8 e 6. Então, a medida do menor ângulo desse triângulo é igual a:
A) 65º.
B) 60º.
C) 55º.
D) 50º.
E) 45º.
Alternativa E.
Sabemos que a soma dos ângulos internos de um triângulo é 180º. Sejam x, y e z os ângulos, temos que:
-
x = 10k
-
y = 8k
-
z = 6k
10k + 8k + 6k = 180
24k = 180
k = 180 : 24
k = 7,5
Sabendo que k = 7,5 e o menor ângulo mede 6k, então 6 · 7,5 = 45.
-
-
Questão 5
Analise o terreno que possui formato triangular a seguir:
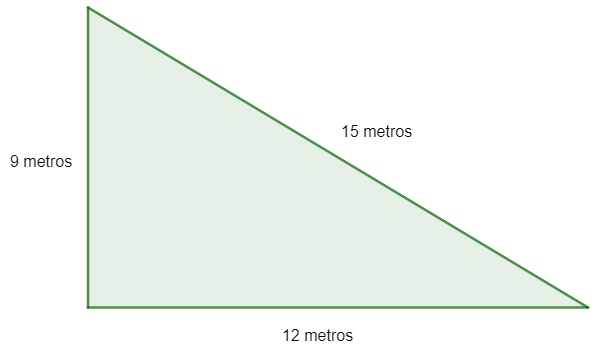
O perímetro desse terreno é de:
A) 27 metros.
B) 36 metros.
C) 54 metros.
D) 60 metros.
E) 62 metros.
Alternativa B.
O perímetro é a soma de todos os lados do triângulo. Calculando o perímetro, temos que:
P = 12 + 9 + 15
P = 36 metros
-
Questão 6
(Facet Concursos) Considere o triângulo ABC em que um ângulo externo, em graus, mede 3x – 15º e os ângulos internos desse triângulo medem 2x + 30º, x + 21º, conforme a figura.
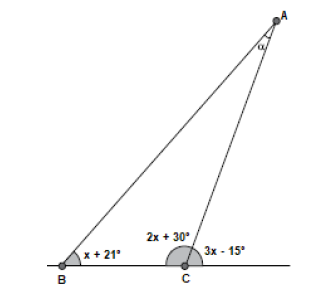
Qual é a medida do ângulo α?
A) 22º
B) 25º
C) 30º
D) 35º
E) 45º
Alternativa C.
Podemos observar que o ângulo interno que mede 2x + 30º com o ângulo externo que mede 3x – 15º são dois ângulos suplementares, ou seja, a soma é igual a 180º.
2x + 30º + 3x – 15º = 180º
5x + 15º = 180º
5x = 180º – 15º
5x = 165º
x = 165 : 5
x = 33
Se x = 33º, sabemos que a soma dos ângulos internos de um triângulo é 180º, então:
x + 21º + 2x + 30º + α = 180º
33º + 21º + 2 · 33º + 30º + α = 180º
54º + 66º + 30º + α = 180º
150º + α = 180º
α = 180º – 150º
α = 30º
-
Questão 7
Uma região é formada por um triângulo escaleno e sua área é de 94 m². Sabendo que um de seus lados mede 11,75 m, então a medida da altura relativa a essa base é de:
A) 8 m.
B) 16 m.
C) 18 m.
D) 20 m.
E) 24 m.
Alternativa B.
Sabemos que a área é igual ao produto entre a base e a altura dividido por 2. Seja h a altura, então:
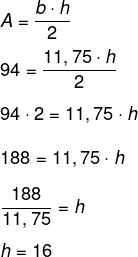
-
Questão 8
Sobre os triângulos, julgue as afirmativas a seguir:
I → Um triângulo escaleno pode ser também um triângulo retângulo.
II → Todo triângulo escaleno possui ângulos internos que somam 180º.
III → O triângulo escaleno não pode possuir ângulos congruentes entre si.
Marque a alternativa correta:
A) Somente a afirmativa I é incorreta.
B) Somente a afirmativa II é incorreta.
C) Somente a afirmativa III é incorreta.
D) Todas as afirmativas são incorretas.
E) Todas as afirmativas são corretas.
Alternativa E.
I → Um triângulo escaleno pode ser também um triângulo retângulo.
II → Todo triângulo escaleno possui ângulos internos que somam 180º.
III → O triângulo escaleno não pode possuir ângulos internos congruentes. Se isso ocorresse, então o triângulo não seria escaleno, mas sim isósceles ou equilátero.
-
Questão 9
Analisando o triângulo escaleno a seguir, calcule o valor de x:
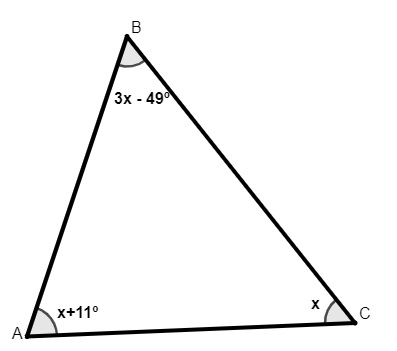
A) 43,6º
B) 44,0º
C) 44,3º
D) 45,2º
E) 46,1º
Alternativa A.
A soma dos ângulos internos é igual a 180º, então:
x + 11º + x + 3x – 49º = 180º
5x – 38º = 180º
5x = 180º + 38º
5x = 218º
x = 218º : 5
x = 43,6º
-
Questão 10
Um triângulo escaleno possui lados medindo 14 cm, 9 cm e x cm. Sabendo que o seu perímetro é igual a 30 cm, então a medida do seu menor lado é:
A) 6 cm.
B) 7 cm.
C) 8 cm.
D) 9 cm.
E) 10 cm.
Alternativa B.
Sabemos que o perímetro é a soma de todos os lados, então:
P = 14 + 9 + x
30 = 14 + 9 + x
30 = 23 + x
30 – 23 = x
x = 7
-
Questão 11
Analise o triângulo a seguir:
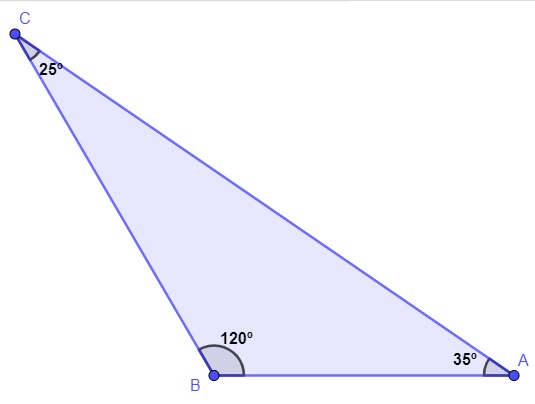
Esse triângulo pode ser classificado como:
A) isósceles e retângulo.
B) escaleno e acutângulo.
C) equilátero e obtusângulo.
D) isósceles e equilátero.
E) escaleno e obtusângulo.
Alternativa E.
O triângulo possui todos os ângulos diferentes. Como consequência, a medida dos lados também é diferente, logo ele é escaleno. Além disso, ele possui um ângulo interno maior que 90º, logo ele é também obtusângulo, então ele é escaleno e obtusângulo.
-
Questão 12
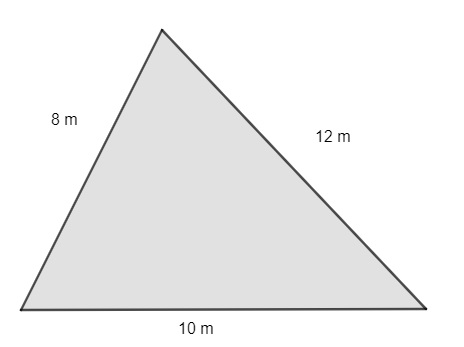
Deseja-se cercar um terreno no formato de um triângulo escaleno com uma cerca de arame farpado. Sabendo que serão dadas 5 voltas de arame e que cada pacote de arame farpado possui um total de 60 metros, a quantidade de pacotes necessários é:
A) 2 pacotes.
B) 3 pacotes.
C) 4 pacotes.
D) 5 pacotes.
Alternativa B.
O perímetro do terreno é:
P = 8 + 12 + 10 = 30
Como vão ser dadas 5 voltas, então 5 · 30 = 180.
Como cada pacote possui 60 metros, para descobrir o total de pacotes necessários, basta realizar a divisão 180 : 60 = 3 pacotes.