Exercícios sobre volume de pirâmide
Para resolver estes exercícios sobre volume de pirâmide, lembre-se de que ele é calculado como um terço do produto entre as medidas da área da base e da altura da pirâmide.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Uma empresa de embalagens criou um perfume cujo frasco tem o formato de uma pirâmide quadrangular regular com 10 cm de lado na base e 12 cm de altura. Qual é o volume máximo, em centímetros cúbicos, de perfume que esse frasco pode comportar?
Alternativa D
O volume de uma pirâmide é dado por \( V=\frac{A_{base}\cdot A l t u r a}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{10_2⸳(12)}3=100⸳4=400 cm^3\)
-
Questão 2
Uma loja de chocolates produz bombons em formato de pequenas pirâmides de base quadrada. Cada bombom tem uma base de 2 cm de lado e uma altura de 3 cm. Se uma caixa contém 50 desses bombons, qual é o volume total de chocolate na caixa?
Alternativa C
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{2^2⸳(3)}3=4=4 cm^3\)(cada um dos chocolates)
Como queremos o volume de 50 dessas pequenas caixas, devemos multiplicar esse resultado por 50, chegando a \(50\cdot4=200 {\rm cm}^3.\)
-
Questão 3
Um aquário tem o formato de uma pirâmide quadrangular regular. Sua base mede 4 metros de lado e a pirâmide tem uma altura de 5 metros. Se o aquário estiver completamente cheio, qual será o volume de água contido nele?
Alternativa C
O volume de uma pirâmide é dado por \( V=\frac{A_{base}\cdot A l t u r a}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{4^2⸳(5)}3=\frac{80}3≈26,67 m^3\)
-
Questão 4
Em uma exposição de arte moderna, um artista apresenta uma obra no formato de uma pirâmide triangular regular, cuja base tem lado de 6 metros e a altura da pirâmide tem 9 metros. Qual é o volume dessa obra de arte?
Alternativa C
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\(A_{base}=\frac{l^2\sqrt3}{4}=\frac{6^2\sqrt3}{4}=9\sqrt{3\ }m^2\)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(V=\frac{9\sqrt3\left(9\right)}{3}=27\sqrt3\ m^3\)
-
Questão 5
Em uma competição de esculturas de areia, um participante decide fazer uma pirâmide triangular regular com 5 metros de lado na base e 8 metros de altura. Qual volume de areia ele precisará, aproximadamente?
Alternativa C
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\(A_{base}=\frac{l^2\sqrt3}{4}=\frac{5^2\sqrt3}{4}=6,25\sqrt3{\ m}^2\)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(V=\frac{6,25\sqrt3\left(8\right)}{3}=\frac{50}{3}\sqrt3\approx29{\ m}^3\)
-
Questão 6
Uma construtora planeja criar um playground em formato de pirâmide. A base será um hexágono regular de 8 m de lado e a altura da pirâmide será de 7 m. Qual será o volume desse playground?
Alternativa B
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\( A_{base}=\frac{6\cdot l^2\sqrt3}{4}=\frac{6\cdot8^2\sqrt3}{4}=96\sqrt3{\ m}^2 \)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(V=\frac{96\sqrt3\left(7\right)}{3}=224\sqrt3\approx388{\ m}^3\)
-
Questão 7
Em um projeto arquitetônico inovador, uma empresa projeta um lobby de hotel em formato de pirâmide triangular regular. Se a base do lobby tem um lado de 10 metros e a altura da pirâmide é de 15 metros, qual será o volume do espaço desse lobby?
Alternativa D
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\( A_{base}=\frac{l^2\sqrt3}{4}=\frac{{10}^2\sqrt3}{4}=25\sqrt3\ m^2 \)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(V=\frac{25\sqrt3\left(15\right)}{3}=125\sqrt3\approx217{\ m}^3=217.000\ litros\)
-
Questão 8
Observe a figura abaixo. A parte da pirâmide representada por 01 possui volume 2 m3.
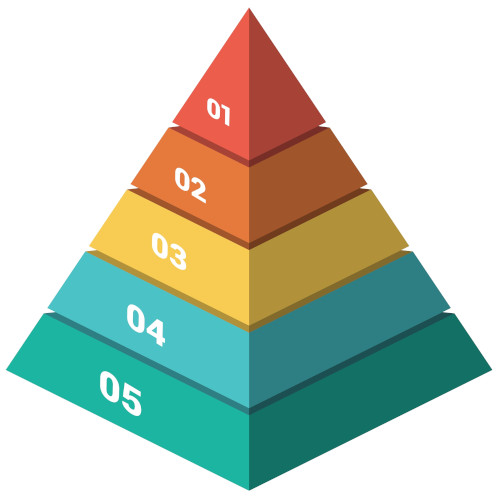
Pirâmide fracionada em cinco partes paralelas e de mesma altura. Determine o volume das 5 partes da figura.
Alternativa E
O exercício requer o volume de 5 partes que, juntas, formam uma pirâmide cujo volume é proporcional ao cubo da razão entre as alturas das 5 partes e a altura da pirâmide 01.
\(\frac{V_5}{V_1}=\left(\frac{H_5}{H_1}\right)^3\)
\(\frac{V_5}{2}=\left(\frac{5h}{h}\right)^3=125\)
\(Logo: V_5=250\ m^3\)
-
Questão 9
Uma pirâmide foi dividida em 7 níveis de mesma altura, conforme a figura abaixo. Sabendo que o volume da figura no nível 1 é igual a 1 dm3, determine o volume da figura do nível 7.
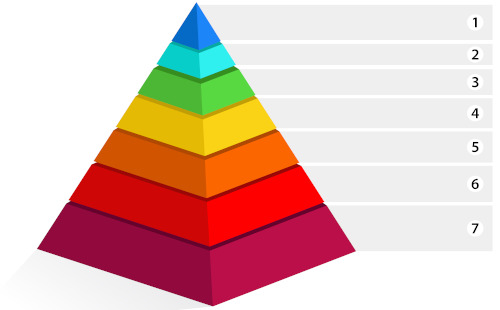
Pirâmide dividida em 7 níveis. Alternativa C
O exercício requer o volume da parte de nível 7, que pode ser obtida pela subtração entre os 7 níveis que formam uma pirâmide e os 6 níveis que formam outra pirâmide.
Chamemos de V7 e V6 os volumes das pirâmides dos 7 níveis e 6 níveis da figura, cujos volumes são proporcionais ao cubo da razão entre as alturas das partes e a altura da pirâmide 01.
\(\frac{V_7}{V_1}=\left(\frac{H_7}{H_1}\right)^3\)
\(\frac{V_7}{1}=\left(\frac{7h}{h}\right)^3=343\)
\(Logo: V_7=343\ {dm}^3\)
\(\frac{V_6}{V_1}=\left(\frac{H_6}{H_1}\right)^3\)
\(\frac{V_6}{1}=\left(\frac{6h}{h}\right)^3=216\)
\(Logo V_6=216{\ dm}^3\)
Concluindo, temos que o volume pedido é \(343-216=127\ {\rm dm}^3\).
-
Questão 10
Uma pirâmide tem como base um trapézio com bases medindo 6 dm e 12 dm e altura de 4 dm. Se a altura da pirâmide é 5 dm, determine seu volume.
Alternativa E
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\( A_{base}=\frac{\left(B+b\right)h}{2}=\frac{(12+6)⸳4}2=36 dm^2 \)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(V=\frac{36⸳(5)}3=60 dm^3\)
-
Questão 11
Uma pirâmide possui como base um trapézio. As bases do trapézio medem 8 dm e 12 dm, e sua altura é de 5 dm. Se a pirâmide tem um volume de 150 dm3, determine a altura dela.
Alternativa C
O volume de uma pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\( A_{base}=\frac{\left(B+b\right)h}{2}=\frac{(12+8)⸳5}2=50 dm^2 \)
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base), temos:
\(150=\frac{50⸳(h)}3\)
\(h=9\ dm\)
-
Questão 12
Observe a figura abaixo e determine seu volume sabendo que suas arestas medem 4 dm.
O octaedro regular é a junção de duas pirâmides. Alternativa D
O exercício pede o volume de um octaedro regular, porém podemos dividir a figura em duas pirâmides de base quadradas cuja altura é a metade da diagonal de um quadrado.
O volume de cada pirâmide é dado por \(V=\frac{A_{base}\cdot A l t u r a}{3}\).
Primeiramente devemos calcular o valor da área da base dessa pirâmide.
\( A_{base}=L^2=4^2=16\ dm^2 \)
A diagonal desse quadrado é dada por \(L\sqrt2=4\sqrt2\), logo, sua altura é \(2\sqrt2\ dm\).
Substituindo os dados fornecidos pelo exercício e os já determinados (área da base e altura da pirâmide), temos:
\(V=\frac{16\cdot(2\sqrt2)}{3}\frac{32\sqrt2}{3}\)
Logo, o volume do octaedro é \(\frac{64\sqrt2}{3}\approx30\ litros\).