Exercícios sobre concentração dos íons em solução
As concentrações em mol/L dos íons Ca2+ e OH- em uma solução aquosa de 0,01 mol/L de Ca(OH)2 são, respectivamente:
-
0,01 e 0,01
-
0,01 e 0,02
-
0,02 e 0,02
-
0,02 e 0,01
-
0,03 e 0,03
Alternativa “b”.
Primeiro escrevemos a equação iônica devidamente balanceada:
Ca(OH)2 → Ca2+ + 2 OH-
Proporção: 1 mol 1 mol 2 mol
Solução: 0,01 mol/L 0,01 mol/L 0,02 mol/L
Uma solução aquosa de sulfato de alumínio, Al2(SO4)3, foi preparada de modo que cada 100 mL de solução tivesse 68,4 g do sal dissolvido a 20ºC. Sabendo que nessa temperatura o grau de dissociação α% do sulfato de alumínio é igual a 60%, a concentração em quantidade de matéria (em mol/L) dos íons Al3+(aq) e SO2-4(aq), respectivamente, é de:
-
4,0 e 6,0
-
2,0 e 3,0
-
2,4 e 3,6
-
2,0 e 6,0
-
4,5 e 5,6
Alternativa “c”.
Primeiro precisamos descobrir a concentração em quantidade de matéria (mol/L) do sal, Al2(SO4)3, na solução:
M = ____m1__
MM . V
M = _____68,4 g________
(342 g/mol) . ( 0,1 L)
M = 2,0 mol/L
Agora podemos descobrir a concentração de cada íon na solução:
Al2(SO4)3(aq) → 2 Al3+(aq) + 3 SO2-4(aq)
Proporção: 1 mol 2 mol 3 mol
Solução: 2,0 mol/L 4,0 mol/L 6,0 mol/L
No entanto, o grau de dissociação (α%) do sulfato de alumínio é igual a 60%:
4,0 mol/L de Al3+(aq) ---------------- 100 %
x------------------------ 60%
x = 60 . 4,0 → x = 2,4 mol/L de íons Al3+(aq)
100
6,0 mol/L de SO2-4(aq) ---------------- 100 %
x------------------------ 60%
x = 60 . 6,0 → x = 3,6 mol/L de íons SO2-4(aq)
100
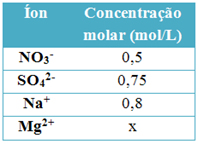
(Fatec-SP) A tabela abaixo mostra o resultado da análise de todos os íons presentes em 1 L de uma solução aquosa, desprezando-se os íons H+ e OH– provenientes da água. Com base nos dados apresentados e sabendo que toda solução é eletricamente neutra, podemos afirmar que a concentração molar dos íons Mg2+ é:
a) 0,4
b) 0,5
c) 0,6
d) 1,0
e) 1,2
Alternativa “c”.
Vamos primeiro escrever todas as equações de dissociação ou ionização:
1 HNO3(aq) → 1 H+(aq) + 1 NO-3(aq)
1 H2SO4(aq) → 2 H+(aq) + 1 SO2-4(aq)
1 NaOH(aq) → 1 Na+(aq) + 1 OH-(aq)
1 Mg(OH)2(aq) → 1 Mg2+(aq) + 2 OH-(aq)
Agora estabelecemos as proporções pelas concentrações dadas:
1 HNO3(aq) → 1 H+(aq) + 1 NO-3(aq)
Proporção: 1 mol 1 mol 1 mol
Solução: 0,5 mol/L 0,5 mol/L 0,5 mol/L
1 H2SO4(aq) → 2 H+(aq) + 1 SO2-4(aq)
Proporção: 1 mol 2 mol 1 mol
Solução: 1,5 mol/L 1,5 mol/L 0,75 mol/L
1 NaOH(aq) → 1 Na+(aq) + 1 OH-(aq)
Proporção: 1 mol 1 mol 1 mol
Solução: 0,8 mol/L 0,8 mol/L 0,8 mol/L
Observe que a solução é neutra e que temos até o momento 2,0 mol/L (0,5 + 1,5) de íons H+. Assim, é preciso a mesma concentração de íons OH-. Até agora só temos 0,8 mol/L destes ânions, para completar 2,0 mol/L ainda faltam 1,2, que é a concentração dos íons da dissociação iônica do Mg(OH)2(aq) .
Agora, sabendo a proporção e a concentração dos íons OH- na equação iônica abaixo, é possível descobrir a concentração em mol/L dos íons Mg2+:
1 Mg(OH)2(aq) → 1 Mg2+(aq) + 2 OH-(aq)
Proporção: 1 mol 1 mol 2 mol
Solução: 0,6 mol/L 0,6 mol/L 1,2 mol/L
(UFSCar-SP) Uma "água dura" contém íons Ca2+ e Mg2+, que interferem na ação do sabão e deixam um resíduo nas paredes de tanques e caldeiras. É possível "amolecer" uma "água dura" adicionando-se substâncias que retiram estes íons e liberam, em seu lugar, íons Na+. Se uma "água dura" contém 0,010 mol/L de Ca2+ e 0,005 mol/L de Mg2+, quantos mols de Na+ são necessários para substituir os íons de cálcio e magnésio em 1,0 . 103 L desta água?
a) 10. b) 15. c) 20. d) 30. e) 40.
Alternativa “d”.
0,010 mol/L de íons Ca2+(aq) ------ 1 L de solução
x---------------- 1,0 . 103 L de solução
x = 1,0 . 103 . 0,010
1
x = 10 mol de íons Ca2+(aq)
0,005 mol/L de íons Mg2+(aq) ------ 1 L de solução
y---------------- 1,0 . 103 L de solução
y = 1,0 . 103 . 0,005
1
y = 5 mol de íons Mg2+(aq)
Total de íons bivalentes a serem substituídos: 10 + 5 = 15 mol.
Como o sódio, Na+, é monovalente, será necessário o dobro de íons desse elemento para substituir os íons Ca2+ e Mg2+, portanto, serão necessários 30 mol de íons Na+(aq).
