Exercícios sobre lei de Hess
Resolva esta lista de exercícios sobre lei de Hess, uma das formas de se calcular a variação de entalpia.
Publicado por: Stéfano Araújo NovaisQuestões
-
Questão 1
(Enem) Glicólise é um processo que ocorre nas células, convertendo glicose em piruvato. Durante a prática de exercícios físicos que demandam grande quantidade de esforço, a glicose é completamente oxidada na presença de O2. Entretanto, em alguns casos, as células musculares podem sofrer um déficit de O2 e a glicose ser convertida em duas moléculas de ácido lático. As equações termoquímicas para a combustão da glicose e do ácido lático são, respectivamente, mostradas a seguir:
C6H12O6 (s) + 6 O2 (g) → 6 CO2 (g) + 6 H2O (l) ΔH = −2800 kJ
CH3CH(OH)COOH (s) + 3 O2 (g) → 3 CO2 (g) + 3 H2O (l) ΔH = −1344 kJ
O processo anaeróbico é menos vantajoso energeticamente porque
A) libera 112 kJ por mol de glicose.
B) libera 467 kJ por mol de glicose.
C) libera 2 688 kJ por mol de glicose.
D) absorve 1 344 kJ por mol de glicose.
E) absorve 2 800 kJ por mol de glicose.
Alternativa A.
O processo anaeróbico consiste na conversão da glicose em duas moléculas de ácido lático:
C6H12O6 (s) → 2 CH3CH(OH)COOH (s)
Para se chegar a essa reação, deve-se manter a primeira reação como está, porém deve-se inverter e dobrar os coeficientes da segunda. Ao se somar as reações, chega-se ao processo anaeróbico.
C6H12O6 (s) + 6 O2 (g) → 6 CO2 (g) + 6 H2O (l) ΔH = −2800 kJ
6 CO2 (g) + 6 H2O (l) → 2 CH3CH(OH)COOH (s) + 6 O2 (g) ΔH = +2688 kJ
___________________________________________________________________________________
C6H12O6 (s) → 2 CH3CH(OH)COOH (s) ΔH = −112 kJ
Assim, percebe-se que o processo anaeróbico é menos vantajoso, pois libera apenas 112 kJ por mol de glicose.
-
Questão 2
(Enem) O benzeno, um importante solvente para a indústria química, é obtido industrialmente pela destilação do petróleo. Contudo, também pode ser sintetizado pela trimerização do acetileno catalisada por ferro metálico sob altas temperaturas, conforme a equação química:
3 C2H2 (g) → C6H6 (l)
A energia envolvida nesse processo pode ser calculada indiretamente pela variação de entalpia das reações de combustão das substâncias participantes, nas mesmas condições experimentais:
- C2H2 (g) + 5/2 O2 (g) → 2 CO2 (g) + H2O (l) ΔH = –310 kcal/mol
- C6H6 (l) + 15/2 O2 (g) → 6 CO2 (g) + 3 H2O (l) ΔH = –780 kcal/mol
A variação de entalpia do processo de trimerização, em kcal, para a formação de um mol de benzeno é mais próxima de
A) –1090.
B) –150.
C) –50.
D) +157.
E) +470.
Alternativa B.
Para se chegar ao processo exigido, deve-se multiplicar a primeira reação por 3 e inverter o sentido da segunda reação. Somando, chegamos à trimerização do acetileno, conforme exigido.
3 C2H2 (g) + 15/2 O2 (g) → 6 CO2 (g) + 3 H2O (l) ΔH = –930 kcal
6 CO2 (g) + 3 H2O (l) → C6H6 (l) + 15/2 O2 (g) ΔH = +780 kcal
________________________________________________________________________________
3 C2H2 (g) → C6H6 (l) ΔH = −150 kcal
-
Questão 3
(Enem) O aproveitamento de resíduos florestais vem tornando cada dia mais atrativo, pois eles são uma fonte renovável de energia. A figura representa a queima de um bio-óleo extraído do resíduo de madeira, sendo ΔH1 a variação de entalpia devido à queima de 1 g desse bio-óleo, resultando em gás carbônico e água líquida, e ΔH2 a variação de entalpia envolvida na conversão de 1 g de água no estado gasoso para o estado líquido.
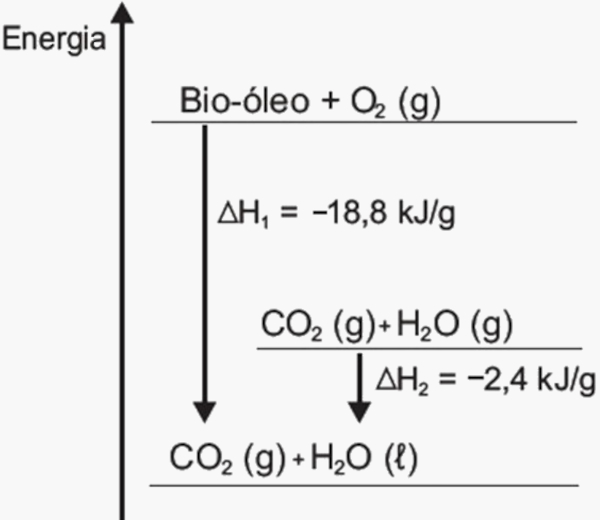
A variação da entalpia, em kJ, para a queima de 5 g desse bio-óleo resultando em CO2 (gasoso) e H2O (gasoso) é:
A) −106.
B) −94,0.
C) −82,0.
D) −21,2.
E) −16,4.
Alternativa C.
A reação exigida é:
Bio-óleo + O2 (g) → CO2 (g) + H2O (g)
Para simplificar, vamos chamar o ΔH dessa reação de ΔH3.
Pelo gráfico, percebe-se que:
ΔH1 = ΔH2 + ΔH3
Portanto:
−18,8 = −2,4 + ΔH3
ΔH3 = −16,4 kJ/g
Porém, a questão exige que seja calculada a variação de entalpia para 5 gramas. Portanto:
1 g ------------------- −16,4 kJ
5 g ------------------- x
x = −16,4 ∙ 5
x = −82,0 kJ
-
Questão 4
(Enem) O ferro é encontrado na natureza na forma de seus minérios, tais como a hematita (α-Fe2O3), a magnetita (Fe3O4) e a wustita (FeO). Na siderurgia, o ferro-gusa é obtido pela fusão de minérios de ferro em altos fornos em condições adequadas. Uma das etapas nesse processo é a formação de monóxido de carbono. O CO (gasoso) é utilizado para reduzir o FeO (sólido), conforme a equação química:
FeO (s) + CO (g) → Fe (s) + CO2 (g)
Considere as seguintes equações termoquímicas:
Fe2O3 (s) + 3 CO (g) → 2 Fe (s) + 3 CO2 (g) ΔH = −25 kJ/mol de Fe2O3
3 FeO (s) + CO2 (g) → Fe3O4 (s) + CO (g) ΔH = −36 kJ/mol de CO2
2 Fe3O4 (s) + CO2 (g) → 3 Fe2O3 (s) + CO (g) ΔH = +47 kJ/mol de CO2
O valor mais próximo de ΔH, em kJ/mol de FeO, para a reação indicada do FeO (sólido) com o CO (gasoso) é
A) −14.
B) −17.
C) −50.
D) −64.
E) −100.
Alternativa B.
Para se chegar à reação pedida, deve-se:
- Dividir a segunda reação por 3.
- Dividir a primeira reação por 2.
- Dividir a terceira reação por 6. Este último passo será importante, pois ele permitirá que, ao se somar as reações, tanto o Fe3O4 (s) quanto o Fe2O3 (s) sejam eliminados.
½ Fe2O3 (s) + 3/2 CO (g) → Fe (s) + 3/2 CO2 (g) ΔH = −12,5 kJ
FeO (s) + 1/3 CO2 (g) → 1/3Fe3O4 (s) + 1/3CO (g) ΔH = −12 kJ
1/3 Fe3O4 (s) + 1/6 CO2 (g) → ½ Fe2O3 (s) + 1/6 CO (g) ΔH = +7,8 kJ
___________________________________________________________________________________
FeO (s) + CO (g) → Fe (s) + CO2 (g) ΔH = −16,7 kJ ≈ −17 kJ
-
Questão 5
O brometo de alumínio, AlBr3, é um importante produto químico para a indústria siderúrgica, uma vez que, quando adicionado ao aço, protege-o de processos de corrosão. Sua síntese é a que se segue:
Al (s) + 3/2 Br2 (l) → AlBr3 (s)
Indique a opção que apresenta corretamente a energia liberada, em quilojoules, necessária para a produção de 1 mol de brometo de alumínio.
Dados:
2 Al (s) + 6 HBr (aq) → 2 AlBr3 (aq) + 3 H2 (g) ∆H = –1061 kJ/mol
HBr (g) → HBr (aq) ∆H = –81 kJ/mol
H2 (g) + Br2 (l) → 2 HBr (g) ∆H = –73 kJ/mol
AlBr3 (s) → AlBr3 (aq) ∆H = –368 kJ/mol
A) 1061
B) 920,5
C) 710
D) 515
E) 305
Alternativa D.
Para se chegar à resposta, deve-se somar as reações após seguintes modificações feitas nelas:
- Dividir a primeira reação por 2.
- Multiplicar a segunda reação por 3, de modo a eliminar o HBr (aq) e o HBr (g).
- Multiplicar a terceira reação por 3/2.
- Inverter a última reação.
Al (s) + 3 HBr (aq) → AlBr3 (aq) + 3/2 H2 (g) ∆H = –530,5 kJ
3 HBr (g) → 3 HBr (aq) ∆H = –243 kJ
3/2 H2 (g) + 3/2 Br2 (l) → 3 HBr (g) ∆H = –109,5 kJ
AlBr3 (aq) → AlBr3 (s) ∆H = +368 kJ
______________________________________________________________________________
Al (s) + 3/2 Br2 (l) → AlBr3 (s) ΔH = −515 kJ
-
Questão 6
O etanol, C2H5OH, é um importante combustível líquido e amplamente utilizado em motores a combustão. Sua grande vantagem é que ele vem de matriz vegetal, a qual minimiza a quantidade de gás carbônico liberada durante a combustão do etanol nos veículos automotores. A reação de combustão completa do etanol é a que se segue.
C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l)
Com base nas equações termoquímicas que se seguem, é possível dizer que o valor da entalpia de combustão do etanol é igual a:
C (graf) + O2 (g) → CO2 (g) ΔH = −394 kJ/mol.
H2 (g) + ½ O2 (g) → H2O (l) ΔH = −286 kJ/mol.
2 C(graf) + 3 H2 (g) + ½ O2 (g) → C2H5OH (l) ΔH = −278 kJ/mol.
A) −228 kJ/mol
B) −242 kJ/mol
C) −1584 kJ/mol
D) –1368 kJ/mol
E) –5471 kJ/mol
Alternativa D.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Multiplicar a primeira reação por 2.
- Multiplicar a segunda reação por 3.
- Inverter a última reação.
2 C (graf) + 2 O2 (g) → 2 CO2 (g) ΔH = −788 kJ
3 H2 (g) + 3/2 O2 (g) → 3 H2O (l) ΔH = −858 kJ
C2H5OH (l) → 2 C(graf) + 3 H2 (g) + ½ O2 (g) ΔH = +278 kJ
_______________________________________________________________________________
C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l) ΔH = −1368 kJ
-
Questão 7
Um dos grandes problemas ambientais que podemos ver em grandes centros urbanos é o aumento da acidez da chuva, fenômeno popularmente conhecido como chuva ácida. O NO2 é um dos acidificantes da água da chuva, uma vez que ele pode produzir o ácido nítrico em contato com a água presente na atmosfera.
3 NO2 (g) + H2O (l) → 2 HNO3 (aq) + NO (g)
A entalpia para o processo descrito é igual a:
Dados:
2 NO (g) + O2 (g) → 2 NO2 (g) ΔH = −116 kJ/mol
N2 (g) + O2 (g) → 2 NO (g) ΔH = +183 kJ/mol
2 N2 (g) + 5 O2 (g) + 2 H2O (l) → 4 HNO3 (aq) ΔH = −256 kJ/mol
A) −137 kJ/mol
B) +137 kJ/mol
C) −274 kJ/mol
D) +274 kJ/mol
E) −68,5 kJ/mol
Alternativa A.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Inverter e multiplicar a primeira reação por 3/2.
- Inverter a segunda reação.
- Dividir por 2 a última reação.
3 NO2 (g) → 3 NO (g) + 3/2 O2 (g) ΔH = +174 kJ
2 NO (g) → N2 (g) + O2 (g) ΔH = −183 kJ
N2 (g) + 5/2 O2 (g) + H2O (l) → 2 HNO3 (aq) ΔH = −128 kJ
_____________________________________________________________________________
3 NO2 (g) + H2O (l) → 2 HNO3 (aq) + NO (g) ΔH = −137 kJ
-
Questão 8
Os alcenos podem ser convertidos em alcanos por meio de reações de hidrogenação. Um exemplo clássico é a hidrogenação do eteno para etano, conforme equação a seguir.
C2H4 (g) + H2 (g) → C2H6 (g)
Utilizando as seguintes equações termoquímicas:
C2H4 (g) + 3 O2 (g) → 2 CO2 (g) + 2 H2O (ℓ) ∆H = −1411,2 kJ/mol
H2 (g) + 1/2 O2 (g) → H2O (ℓ) ∆H = −285,8 kJ/mol
C2H6 (g) + 7/2 O2 (g) → 2 CO2 (g) + 3 H2O (ℓ) ∆H = −1560,7 kJ/mol
É possível dizer que, na hidrogenação de 5 mols de eteno, a variação de entalpia é igual a:
A) −681,5 kJ
B) +681,5 kJ
C) −136,3 kJ
D) +136,3 kJ
E) −1363,0 kJ
Alternativa C.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Manter a primeira reação.
- Manter a segunda reação.
- Inverter a terceira reação.
C2H4 (g) + 3 O2 (g) → 2 CO2 (g) + 2 H2O (ℓ) ∆H = −1411,2 kJ
H2 (g) + 1/2 O2 (g) → H2O (ℓ) ∆H = −285,8 kJ
2 CO2 (g) + 3 H2O (ℓ) → C2H6 (g) + 7/2 O2 (g) ∆H = +1560,7 kJ
_______________________________________________________________________________
C2H4 (g) + H2 (g) → C2H6 (g) ΔH = −136,3 kJ
-
Questão 9
O trióxido de enxofre pode se decompor segundo a reação:
SO3 (g) → SO2 (g) + ½ O2 (g)
Com base nas equações termoquímicas que se seguem, determine a variação de entalpia para a decomposição do trióxido de enxofre, em kJ.
S (s) + O2 (g) → SO2 (g) ΔH = –297 kJ/mol
S (s) + 3/2 O2 (g) → SO3 (g) ΔH = –395 kJ/mol
A) −692 kJ
B) −384 kJ
C) +384 kJ
D) −98 kJ
E) +98 kJ
Alternativa E.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Manter a primeira reação.
- Inverter a segunda reação.
S (s) + O2 (g) → SO2 (g) ΔH = –297 kJ
SO3 (g) → S (s) + 3/2 O2 (g) ΔH = +395 kJ
________________________________________________________
SO3 (g) → SO2 (g) + ½ O2 (g) ΔH = +98 kJ
-
Questão 10
A combustão da amina pode ser demonstrada por meio da seguinte reação química:
4 NH3 (g) + 3 O2 (g) → 2 N2 (g) + 6 H2O (g)
Considere as seguintes equações termoquímicas envolvendo a amônia:
4 NH3 (g) + 7 O2 (g) → 4 NO2 (g) + 6 H2O (g) ΔH = –1132 kJ
6 NO2 (g) + 8 NH3 (g) → 7 N2 (g) + 12 H2O (g) ΔH = –2740 kJ
A energia liberada na queima de 1 mol de amônia é:
A) −317 kJ
B) −402 kJ
C) −968 kJ
D) −1268 kJ
E) −1608 kJ
Alternativa A.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Multiplicar a primeira reação por 3/7, pois isso acerta a quantidade de O2 (g) desejada.
- Multiplicar a segunda reação por 2/7, pois isso acerta a quantidade de N2 (g) desejada.
12/7 NH3 (g) + 3 O2 (g) → 12/7 NO2 (g) + 18/7 H2O (g) ΔH = –485 kJ
12/7 NO2 (g) + 16/7 NH3 (g) → 2 N2 (g) + 24/7 H2O (g) ΔH = –783 kJ
__________________________________________________________________________
4 NH3 (g) + 3 O2 (g) → 2 N2 (g) + 6 H2O (g) ΔH = −1268 kJ
Porém a reação dada é para 4 mols de NH3, enquanto o exercício exige que seja calculada a energia para apenas 1 mol de NH3. Assim:
4 mols NH3 ------------------------ −1268 kJ
1 mol NH3 ------------------------- x
4 ∙ x = −1268
x = −317 kJ
-
Questão 11
O metano, gás natural e de fórmula CH4, pode ser obtido via hidrogenação da grafita.
C (graf.) + 2 H2 (g) → CH4 (g)
A alternativa que contém a quantidade de energia liberada, em kcal, na produção de 1 mol de metano é:
Dados:
C (graf) + O2 (g) → CO2 (g) ΔH = −94,1 kcal
H2 (g) + ½ O2 (g) → H2O (l) ΔH = −68,3 kcal
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l) ΔH = −212,8 kcal
A) 89,5 kcal
B) 17,9 kcal
C) 50,4 kcal
D) 252,0 kcal
E) 179 kcal
Alternativa B.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Manter a primeira reação.
- Duplicar a segunda reação.
- Inverter a terceira reação.
C (graf) + O2 (g) → CO2 (g) ΔH = −94,1 kcal
2 H2 (g) + O2 (g) → 2 H2O (l) ΔH = −136,6 kcal
CO2 (g) + 2 H2O (l) → CH4 (g) + 2 O2 (g) ΔH = +212,8 kcal
__________________________________________________________________________
C (graf.) + 2 H2 (g) → CH4 (g) ΔH = −17,9 kcal
-
Questão 12
A formação do carbonato de cálcio pode ser feita por meio da neutralização do hidróxido de cálcio com ácido carbônico, conforme reação que se segue.
H2CO3 (aq) + Ca(OH)2 (aq) → CaCO3 (s) + 2 H2O (l)
Com base nas entalpias-padrão de reação, em kJmol-1, que se seguem:
CaO (s) + CO2 (g) → CaCO3 (s) ΔH° = −183,3 kJ/mol
CaO (s) + H2O (l) → Ca(OH)2 (aq) ΔH = −82,4 kJ/mol
CO2 (g) + H2O (l) → H2CO3 (aq) ΔH° = −20,5 kJ/mol
Calcule a variação de entalpia para a reação de produção do carbonato de cálcio por meio da neutralização entre o ácido carbônico e o hidróxido de cálcio.
A) −80,4 kJ
B) −224,7 kJ
C) −160,8 kJ
D) −183,3 kJ
E) −286,2 kJ
Alternativa A.
Para se chegar à reação de interesse, antes de somar as reações dadas, deve-se:
- Manter a primeira reação.
- Inverter a segunda reação.
- Inverter a terceira reação.
CaO (s) + CO2 (g) → CaCO3 (s) ΔH° = −183,3 kJ
Ca(OH)2 (aq) → CaO (s) + H2O (l) ΔH = +82,4 kJ
H2CO3 (aq) → CO2 (g) + H2O (l) ΔH° = +20,5 kJ
______________________________________________________________________________
H2CO3 (aq) + Ca(OH)2 (aq) → CaCO3 (s) + 2 H2O (l) ΔH = −80,4 kJ