Exercícios sobre comprimento de arco
Resolva esta lista de exercícios sobre comprimento de arco e teste seus conhecimentos sobre o assunto.
Perguntas
Questão: 1
Qual é o comprimento de um arco cujo ângulo central é de 45º, sabendo que o raio da circunferência mede 2 cm?
A) π
B) π2
C) π4
D) π6
E) π8
Questão: 2
Uma circunferência tem comprimento medindo 6π cm. Se existir um arco com ângulo de 60º, então o valor da medida do comprimento desse arco é de:
A) π4
B) π3
C) π2
D) π
E) 2π
Questão: 3
Analise a imagem a seguir, e calcule a imagem do arco que vai do ponto B até o ponto B’, sabendo que o raio mede 3 u.m.
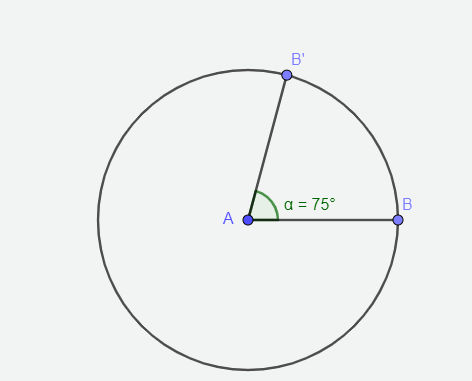
A) 2π
B) 1,5π
C) 0,75π
D) 0,5π
E) 0,25π
Questão: 4
Se, numa circunferência, o comprimento mede 21 metros, e sabendo que existe um ângulo central cuja medida do comprimento de um arco é de 5,25 metros, então a medida desse ângulo é igual a:
A) 30º
B) 45º
C) 60º
D) 75º
E) 90º
Questão: 5
Sabendo que um arco de uma circunferência mede 4,2 radianos, e que o seu raio mede 10 cm, então a medida do comprimento desse arco é igual a:
A) 14,2 cm
B) 28,4 cm
C) 32,0 cm
D) 42,0 cm
E) 56,0 cm
Qual é o ângulo central do arco da circunferência, sabendo que o comprimento da circunferência é de 6π e o comprimento do arco mede 34π?
A) 30º
B) 45º
C) 60º
D) 75º
E) 90º
Qual é o comprimento da circunferência cuja medida do comprimento de um arco com ângulo central igual a 30º é igual a 3π cm?
A) 36π cm
B) 18π cm
C) 9π cm
D) 6π cm
E) 3π cm
Considerando um círculo com 8 cm de diâmetro, e traçando um ângulo central de 120º, a medida do arco desse ângulo é igual a:
A) 8π cm
B) 2π cm
C) 23π cm
D) 43π cm
E) 83π cm
Um pêndulo de 20 cm de comprimento oscila entre A e A’ e percorre um arco cujo ângulo central é de 20º. Aproximadamente, o comprimento da trajetória descrita pela sua extremidade entre A e A’ é de:
(use π=3)
A) 3,6 cm
B) 4,8 cm
C) 6,7 cm
D) 7,2 cm
E) 8,0 cm
O comprimento do arco maior na imagem, em centímetros, sabendo que o raio mede 5 cm, é:
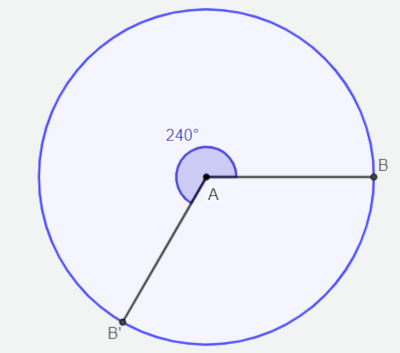
A) 12π
B) 23π
C) 53π
D) 103π
E) 154π
Questão: 11
Qual é o comprimento do arco BC, sabendo que o comprimento da circunferência é igual a 24 cm:
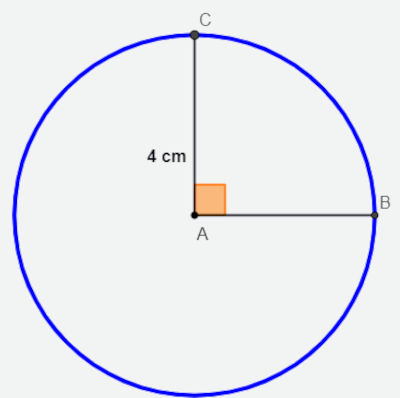
A) 6 cm
B) 12 cm
C) 16 cm
D) 24 cm
E) 30 cm
Questão: 12
Qual é o comprimento de um arco cujo ângulo central é de 40º, sabendo que o raio da circunferência mede 9 cm?
A) π
B) π2
C) π4
D) π6
E) π8
Respostas
Questão: 1
Alternativa B
Sabemos que o comprimento da circunferência toda é dado por C= 2πr. Como queremos somente uma parte dela, temos que:
l=θ ⋅ 2πr360
l=45 ⋅ 2π⋅2360
l=180π360
l=π2
Questão: 2
Alternativa D
Sabemos que:
C = 2πr = 6π
Então temos que:
l=θ⋅2πr360
l=60⋅6π360
l=360π360
l=π
Questão: 3
Alternativa B
Sabemos que r = 3 e que θ=75, então temos que:
l=θ⋅2πr360
l=75 ⋅ 2π ⋅ 3360
l=450π360
l=1,5π
Questão: 4
Alternativa E
Utilizando a fórmula, sabemos que l = 5,25 e que 2πr=21. Então temos que:
l=θ⋅2πr360
5,25=θ ⋅ 21360
5,25⋅360=θ ⋅ 21
1890=θ ⋅ 21
θ=189021
\theta = 90 º
Questão: 5
Alternativa D
Sabemos que:
l = \theta \cdot \pi
l = 10 \cdot 4,2
l = 42 cm
Questão: 6
Alternativa B
Substituindo na fórmula, temos que:
l= \frac{\theta \cdot2\pi r}{360}
\frac {3}{4}\pi= \frac{\theta \cdot6\pi}{360}
Simplificando o π dos dois lados, temos que:
\frac {3}{4}= \frac{6\ \theta}{360}
6\ \theta \cdot 4 = 3 \cdot 360
24\ \theta = 1080
\theta = \frac {1080}{24}
\theta = 45º
Questão: 7
Alternativa A
Sabemos que l = 3π e que o ângulo central mede 30º. Ao dividirmos 360º por 30º, temos que 360º : 30º = 12, sendo assim, sabemos que o comprimento da circunferência toda é 12 vezes maior que o arco, então temos que:
C= 12⋅3π =36π
Questão: 8
Alternativa E
Para calcular o raio, dividiremos o diâmetro por dois, logo, temos que:
r = 8 : 2 = 4
Sabemos que theta = 120°. Temos que:
l= \frac{120 \cdot2\pi 4}{360}
l= \frac{960\pi}{360}
l= \frac{8}{3}\pi
Questão: 9
Alternativa C
Substituindo na fórmula, temos que:
l= \frac{\theta \cdot2\pi r}{360}
l= \frac{20 \cdot2\pi\cdot 20}{360}
l= \frac{800\pi}{360}
l= \frac{20}{9}\pi
l= \frac{20\cdot 3}{9}
l= \frac{60}{9}
l= 6,7 cm
Questão: 10
Alternativa D
Calculando o comprimento do arco, temos que:
l= \frac{240 \cdot2\pi\cdot 5}{360}
l= \frac{1200\pi}{360}
l= \frac{10}{3}\pi
Questão: 11
Alternativa A
Sabemos que 360 : 90 = 4. Sendo assim, o arco é igual à quarta parte do comprimento da circunferência:
24 : 4 = 6 cm
Questão: 12
Alternativa A
l= \frac{\theta \cdot2\pi r}{360}
l= \frac{40 \cdot\pi\cdot 9}{360}
l= \frac{360\pi}{360}
l= \pi cm
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-comprimento-um-arco.htm