Exercícios sobre Regra de Três Composta
Esta lista de exercícios vai testar seus conhecimentos sobre regra de três composta, assunto que envolve as grandezas direta e inversamente proporcionais.
Perguntas
Questão: 1
Para realizar o acabamento de um condomínio fechado, 2 pedreiros foram contratados. Sabendo que eles conseguiram fazer o reboco de 48 m² por dia, trabalhando 6 horas diárias, qual seria a produtividade se fossem contratados mais 4 pedreiros e o tempo de trabalho de todos os pedreiros fosse de 4 horas por dia?
A) 72 m²
B) 80 m²
C) 92 m²
D) 96 m²
E) 100 m²
Questão: 2
Para produção de um determinado tipo de peça em uma empresa, 5 máquinas com produtividades idênticas produzem 260 peças em 5 dias, operando 4 horas por dia. Sabendo que duas máquinas deram defeito, qual será a quantidade de peças produzidas durante 10 dias se as máquinas restantes operarem durante 10 horas?
A) 680
B) 780
C) 850
D) 900
E) 920
Questão: 3
A quantidade de ração utilizada para alimentar 10 cachorros em um canil, durante 15 dias, é de 60 kg. Caso cheguem mais 8 cachorros no canil, quantos dias 80% dessa ração duraria aproximadamente?
A) 6 dias
B) 5 dias
C) 4 dias
D) 8 dias
E) 10 dias
Questão: 4
Em uma construção, 4 pedreiros levam 18 dias para realizar a construção de um muro com 2 metros de altura. Caso houvesse 2 pedreiros a mais e a altura do muro fosse de 4 metros, quanto tempo esses pedreiros levariam?
A) 20 dias
B) 24 dias
C) 28 dias
D) 30 dias
E) 22 dias
Questão: 5
Quatro torneiras enchem um reservatório em 10 horas. Quantas horas levarão 7 torneiras para encher 2 tanques?
A) Entre 8 e 9 horas
B) Entre 9 e 10 horas
C) Entre 10 e 11 horas
D) Entre 11 e 12 horas
E) Entre 12 e 13 horas
Questão: 6
Em uma fábrica de perfumes, 3 máquinas produzem 900 perfumes em 12 dias. Quantos dias serão necessários para 8 máquinas produzirem 1200 perfumes?
A) 2
B) 4
C) 6
D) 8
E) 10
Questão: 7
Em uma plantação de milho, duas colheitadeiras carregam 5 caminhões durante 4 horas. Determine quanto tempo 5 colheitadeiras levariam para carregar 15 caminhões.
A) Entre 3 e 4 horas
B) Entre 4 e 5 horas
C) Entre 5 e 6 horas
D) Entre 7 e 8 horas
E) Mais que 8 horas
Questão: 8
Sabendo que 4 impressoras iguais produzem 800 panfletos em 40 minutos, quantos folhetos seriam produzidos em 1 hora havendo 6 dessas impressoras?
A) 1000
B) 1200
C) 1400
D) 1600
E) 1800
Questão: 9
(Enem 2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e, nos primeiros 10 dias, trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.
Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
A) 920 kg.
B) 800 kg.
C) 720 kg.
D) 600 kg.
E) 570 kg.
Questão: 10
(Enem 2017) Uma indústria tem um setor totalmente automatizado. São quatro máquinas iguais, que trabalham simultânea e ininterruptamente durante uma jornada de 6 horas. Após esse período, as máquinas são desligadas por 30 minutos para manutenção. Se alguma máquina precisar de mais manutenção, ficará parada até a próxima manutenção.
Certo dia, era necessário que as quatro máquinas produzissem um total de 9 000 itens. O trabalho começou a ser feito às 8 horas. Durante uma jornada de 6 horas, produziram 6 000 itens, mas na manutenção observou-se que uma máquina precisava ficar parada. Quando o serviço foi finalizado, as três máquinas que continuaram operando passaram por uma nova manutenção, chamada manutenção de esgotamento.
Em que horário começou a manutenção de esgotamento?
A) 16 h 45 min
B) 18 h 30 min
C) 19 h 50 min
D) 21 h 15 min
E) 22 h 30 min
Questão: 11
(BNB – FGV) Em uma agência bancária, dois caixas atendem em média seis clientes em 10 minutos. Considere que, nessa agência, todos os caixas trabalham com a mesma eficiência e que a média citada sempre é mantida. Assim, o tempo médio necessário para que cinco caixas atendam 45 clientes é de:
A) 45 minutos.
B) 30 minutos.
C) 20 minutos.
D) 15 minutos.
E) 10 minutos.
Questão: 12
(Enem 2013) Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Essa indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser igual a
A) 2
B) 4
C) 5
D) 8
E) 9
Respostas
Questão: 1
Alternativa D.
As grandezas são quantidade de pedreiros, horas trabalhadas e área rebocada por dia. Sabemos que a incógnita está na área, então analisaremos a proporcionalidade entre ela e as demais grandezas.
-
Comparando a área com a quantidade de pedreiros, quanto maior a quantidade de pedreiros, maior será a área rebocada, logo as grandezas são diretamente proporcionais.
-
Comparando a área com o tempo de serviço por dia, se o tempo for maior, então a área rebocada nesse dia também será maior, sendo assim essas grandezas também são diretamente proporcionais.
Agora construiremos a tabela com as grandezas.

Construindo a regra de três, temos que:
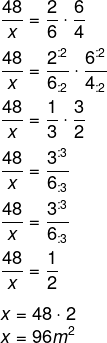
Questão: 2
Alternativa B.
Analisando a situação, há 4 grandezas: quantidade de peças, dias, horas e quantidade de máquinas. A grandeza que possui a incógnita são as peças, então vamos analisar a proporcionalidade dela em relação às demais grandezas.
-
Analisando as grandezas peças e dias, e também peças e horas, é fácil perceber que, quanto maior o tempo, seja em dia, seja em horas, maior será a quantidade de peças produzidas. Sendo assim, as grandezas são diretamente proporcionais.
-
O mesmo acontece com peças e máquinas. Se tivermos mais máquinas, maior será a quantidade de peças produzidas, logo as grandezas são diretamente proporcionais.
Construindo a tabela, temos que:

Montando a regra de três, temos que:
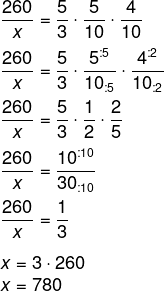
Alternativa A.
As grandezas são: quantidade de cachorros, dias e peso.
Comparando as grandezas, sabemos que a incógnita está na grandeza dias, então vamos analisar a proporcionalidade entre dias e as demais grandezas.
-
As grandezas dias e peso são diretamente proporcionais, pois, quanto maior a quantidade de ração, maior será a duração dela em dias.
-
As grandezas dias e quantidade de cachorros são inversamente proporcionais, pois, quanto menor a quantidade de cachorros, maior a quantidade de dias em que a ração vai durar.
Calculando o total de ração, temos que:
80% de 60 = 0,8 · 60 = 48 kg
Agora vamos construir a tabela:

Invertendo as grandezas quantidade de cachorros e montando a regra de três, temos que:
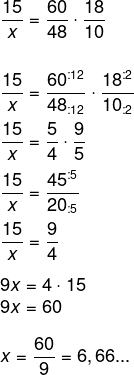
Alternativa B.
As grandezas são: pedreiros, dias e altura. A incógnita está na grandeza dias, então vamos analisar a proporcionalidade entre ela e as demais grandezas.
-
Comparando pedreiros e dias, caso seja diminuída a quantidade de pedreiros, a quantidade de dias para construir o muro será maior, logo pedreiros e dias são inversamente proporcionais.
-
Comparando dias e altura, se aumentarmos a altura do muro, consequentemente a quantidade de dias necessários para construir esse muro também aumentará.
Agora construiremos a tabela:

Montando a equação e invertendo a razão dos pedreiros, temos que:
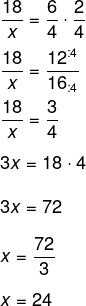
Questão: 5
Alternativa D.
As grandezas são: quantidade de torneiras, tempo e quantidade de tanques. Sabendo que a incógnita está na grandeza tempo, temos que:
-
tempo e torneiras são inversamente proporcionais, pois, quanto maior a quantidade de torneiras, menor será o tempo.
-
tempo e tanques são diretamente proporcionais, pois, quanto maior o tempo, maior será a quantidade de tanques preenchidos.
Construindo a tabela:

Montando as razões, vamos inverter a razão das torneiras, então temos que:
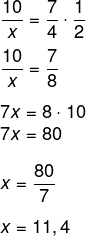
Questão: 6
Alternativa C.
As grandezas são: quantidade de máquinas, quantidade de perfumes e dias. A incógnita está na grandeza tempo, então vamos analisar a proporção entre ela e as demais grandezas.
-
Tempo e máquinas são inversamente proporcionais, pois, se eu aumentar o tempo, a quantidade de máquinas necessárias para realizar uma mesma produção diminuirá.
-
Tempo e quantidade de perfumes são grandezas diretamente proporcionais, pois, se eu aumento o tempo, a quantidade de perfumes produzidos também aumenta.
Construindo a tabela, temos que:

Montando as razões, vamos inverter a razão das máquinas, então temos que:
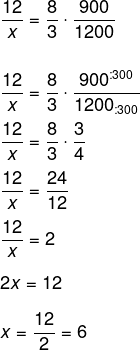
Alternativa B.
As grandezas são: quantidade de colheitadeiras, quantidade de caminhões e tempo. Sabendo que a incógnita está na grandeza tempo, vamos analisar sua proporção com as demais.
-
Tempo e colheitadeira são inversamente proporcionais, pois, se aumentamos o tempo, precisamos de menos colheitadeiras para preencher os caminhões.
-
Tempo e caminhões são diretamente proporcionais, pois, se aumentamos o tempo, a quantidade de caminhões cheios também aumentará.
Construindo a tabela, temos que:

Montando a regra de três e invertendo a razão da colheitadeira, temos que:
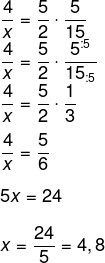
Alternativa E.
As grandezas são: quantidade de impressoras, quantidade de panfletos e tempo.
A incógnita está na grandeza panfletos, então, analisando a proporcionalidade dela com as demais, temos que:
-
panfletos e impressoras são diretamente proporcionais, pois, se aumentamos a quantidade de impressoras, a quantidade de panfletos produzidos aumenta também.
-
Panfletos e tempo também são diretamente proporcionais, pois, se aumentamos o tempo, a quantidade de panfletos produzidos também aumenta.
Lembrando que 1 hora tem 60 minutos e montando a tabela, temos que:

Escrevendo a regra de três:
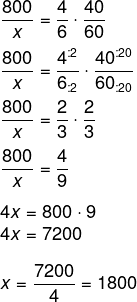
Questão: 9
Alternativa A.
As grandezas são: quantidade de alunos, tempo e peso. Sabendo que o peso é a nossa incógnita, vamos comprar as grandezas.
-
Peso e quantidade de alunos são grandezas diretamente proporcionais, pois, quanto maior a quantidade de alunos, maior será a quantidade de alimentos arrecadada.
-
Comparando peso e dias, quanto maior a quantidade de dias, maior será a quantidade arrecadada também, logo peso e dias são grandezas diretamente proporcionais também.
Para facilitar, sabemos que eles trabalharam 10 dias, durantes 3 horas por dia, então trabalharam 30 horas.
Agora eles vão trabalhar durante 20 dias, 4 horas por dia, ou seja, 80 horas. Se a coleta foi de 12 kg por dia, ao final dos 10 dias foram coletados 120 kg. Como eram 20 alunos e foram acrescentados mais 30, então teremos 50 alunos.
Montando a tabela, temos que:

Calculando a regra de três:
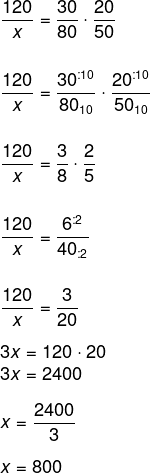
Como nos 10 primeiros dias foram arrecadados 120 kg e nos outros 20, 800 kg, então o total foi de:
120 + 800 = 920
Questão: 10
Alternativa B
As grandezas são: tempo, itens e quantidade de máquinas.
Comparando as grandezas, temos que:
-
quanto maior o tempo, maior será a quantidade de itens produzidos, então tempo e itens são diretamente proporcionais.
-
quanto maior o tempo, menor será a quantidade de máquinas necessárias, então tempo e máquinas são inversamente proporcionais.
Faltam 3000 itens, já que 6000 foram produzidos, e a meta é 9000. Além disso, há 3 máquinas para atender a essa demanda. Montando a tabela, temos que:

Vamos inverter a razão das máquinas, então temos que:
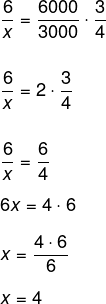
Somando os termos: se o trabalho iniciou-se às 8 horas, foram 6 horas com as 4 máquinas, mais 30 minutos de manutenção, mais as últimas 4 horas com as três máquinas, logo o trabalho vai se encerrar às 18 horas e 30 minutos.
Questão: 11
Alternativa B.
As grandezas envolvidas são caixas, clientes e tempo. A grandeza que possui a incógnita é o tempo, então vamos compará-la com as demais.
-
Tempo e clientes: se aumentamos o número de clientes, aumentamos o tempo para atendê-los, fixando a quantidade de caixas, logo as grandezas quantidade de clientes e tempo são diretamente proporcionais.
-
Tempo e caixas: se diminuímos o tempo, a quantidade de caixas necessários para atender a mesma quantidade de cliente será maior, logo tempo e caixas são grandezas inversamente proporcionais. Montado a tabela, teremos:

Invertendo a fração que representa a quantidade de caixas, temos que:
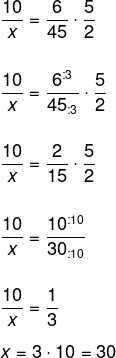
Alternativa C.
Primeiro vamos identificar as grandezas envolvidas: capacidade, quantidade de ralos e tempo, e a incógnita é a quantidade de ralos. Agora vamos analisar a proporção entre quantidade de ralos e as demais grandezas.
-
Ao comparar quantidade de ralos e tempo, fixando uma mesma capacidade para o reservatório, quanto maior a quantidade de ralos, menor será o tempo gasto, logo ralo e tempo são inversamente proporcionais.
-
Ao comparar quantidade de ralos e capacidade, fixando um mesmo tempo, se eu aumento a quantidade de ralos, posso aumentar a capacidade. Assim sendo, quantidade de ralos e capacidade são diretamente proporcionais. A tabela ficará assim:

Invertendo a fração na grandeza tempo, temos que:
![]()
Vamos simplificar o máximo possível cada uma dessas frações:
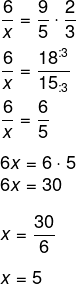
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-regra-tres-composta.htm