Exercícios sobre Números Complexos
Para resolver estes exercícios sobre números complexos, é importante conhecer as definições da parte imaginária e da parte real, além das potências de i.
Perguntas
Questão: 1
Calcule a expressão: (1 + i)2
i
Resolva a equação do 2º grau: x² – 4x + 5 = 0
Questão: 3
(PUC) Na soma S = 1 + i + i2 + i3 + i4 + i5, onde i = √ –1, o valor de S é:
a) 2 – i
b) 1 – i
c) 2 + i
d) 1 + i
Questão: 4
(Cefet – MG) O valor da expressão .jpg) quando x = i (unidade imaginária) é:
quando x = i (unidade imaginária) é:
a) (i + 1)
b) – (i – 1)
c) (i + 1)
2
d) (i – 1)
2
e) – (i – 1)
2
Respostas
Questão: 1
Através dos produtos notáveis, podemos desenvolver o numerador da fração:
(1 + i)²
i
1 + 2i + i²
i
1 + 2i + (– 1)
i
2i
i
2
Portanto, o resultado da expressão é 2.
Questão: 2
Utilizaremos a fórmula de Bhaskara para encontrar o valor de x:
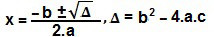
Δ = (– 4)² – 4.1.5
Δ = 16 – 20
Δ = – 4
Mesmo com o resultado negativo de delta, continuaremos a procura pelo valor de x:
x = – (– 4) ± √– 4
2.1
x = 4 ± √4.(–1)
2
x = 4 ± 2√–1
2
x = 4 ± 2i
2
x = 2 ± i
x' = 2 + i
x'' = 2 – i
Temos dois valores para x, são eles 2 + i e 2 – i.
Questão: 3
Vamos calcular o valor de cada uma das potências de i:
i2 = (√–1)2 = –1
i3 = i . i2 = – 1. i = – i
i4 = i2 . i2 = (– 1). (– 1) = 1
i5 = i . I4 = i. 1 = i
Vamos agora calcular o valor de S:
S = 1 + i + i2 + i3 + i4 + i5
S = 1 + i – 1 – i + 1 + i
S = 1 + i
Portanto, a alternativa correta é a letra d.
Questão: 4
Para resolver essa questão, substituiremos x por i em .jpg) :
:
i² – 1
i³ – 1
– 1 – 1
– i – 1
– 2
– 1 – i
Multiplicando a fração pelo conjugado do denominador, temos:
– 2 . – 1 + i
– 1 – i – 1 + i
2 – 2i
1 – i²
2(1 – i)
1 – (– 1)
2(1 – i)
2
1 – i
A resposta encontrada pode ser escrita também como – (i – 1), que é igual a 1 – i. Portanto, a alternativa correta é a letra b.
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-numeros-complexos.htm