Perguntas

Questão: 1

Durante a comemoração do aniversário do Heitor, foram consumidos $\frac{3}{5}$ do bolo. No outro dia, pela manhã, Heitor comeu $\frac{1}{2}$ do que restava do bolo. Sendo assim, a fração que representa a quantidade de bolo que ainda resta é:

A) 2/3

B) 1/4

C) 1/5

D) 2/5

E) 1/10

Questão: 2

Para incentivar a prática esportiva na escola, foi realizada uma pesquisa com os estudantes sobre qual é o esporte favorito dos estudantes da instituição. Dos 350 estudantes entrevistados, 200 afirmaram que o esporte favorito é futebol, 120 voleibol e o restante afirmou que prefere outros esportes. Nessas condições, a fração que representa a razão entre o total de estudantes que preferem futebol e o total de estudantes entrevistados é:

A) 2/5

B) 1/6

C) 1/3

D) 2/7

E) 4/7

Questão: 3

Em uma sala, 60 alunos realizaram uma prova de Geografia. Deles, 2/5 tiraram nota acima de oito, 1/3 tirou entre seis e oito e o restante tirou abaixo de seis. Sabendo que a média dessa escola é 6, a quantidade de estudantes que tiraram nota abaixo da média foi de:

A) 16

B) 15

C) 12

D) 9

E) 8

Questão: 4

Analise as frações a seguir:

I. $\frac{9}{5}$

II. $\frac{9}{3}$

III. $\frac{1}{3}$

As frações listadas podem ser classificadas respectivamente como:

A) Própria, impropria e aparente

B) Própria, aparente e imprópria

C) Imprópria, própria e aparente

D) Imprópria, aparente e própria

E) Aparente, imprópria e própria

Questão: 5

Uma sala de aula possui 24 alunos, sendo que 8 são meninas e 16 são meninos. A fração que representa a quantidade de meninas em relação ao todo é:

A) 1/3

B) 1/4

C) 2/3

D) 1/2

E) 4/3

Questão: 6

Durante a eleição de síndico de um condomínio, 1/3 dos moradores votou no candidato A e 2/5 votaram no candidato B. A fração que representa o número de eleitores que não votaram em nenhum dos candidatos é:

A) 11/15

B) 1/15

C) 2/15

D) 1/5

E) 4/15

Questão: 7

Uma herança será repartida entre 3 herdeiros. Mariana é uma das herdeiras, e ficará com 1/4 dessa herança. Matheus ficará com 2/5. O restante é do Jovair. Então a fração que representa a parte da herança do Jovair é:

A) 3/20

B) 7/20

C) 13/20

D) 7/10

E) 13/10

Questão: 8

Julgue as afirmativas as seguir:

I – Toda fração imprópria é um número maior que 1.

II – Toda fração própria é um número menor que 1.

III – Toda fração aparente é um número inteiro.

Marque a alternativa correta:

A) Somente a I é falsa

B) Somente a II é falsa

C) Somente a III é falsa

D) Todas são verdadeiras

Questão: 9

(Enem 2020) Foi feita uma pesquisa sobre a escolaridade dos funcionários de uma empresa. Verificou-se que 1/4 dos homens que ali trabalham têm o ensino médio completo, enquanto 2/3 das mulheres que trabalham na empresa têm o ensino médio completo. Constatou-se, também, que entre todos os que têm o ensino médio completo, metade são homens.

A fração que representa o número de funcionários homens em relação ao total de funcionários dessa empresa é

A) 1/8

B) 3/11

C) 11/24

D) 2/3

E) 8/11

Questão: 10

(Enem 2016) No tanque de um certo carro de passeio cabem até 50L de combustível, e o rendimento médio desse carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km, o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir.

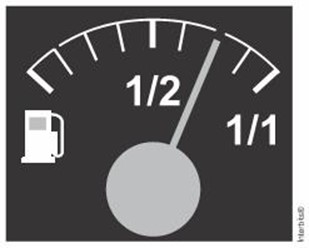
Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.

Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?

A) 570

B) 500

C) 450

D) 187

E) 150

Questão: 11

(Enem 2020) Uma empresa de ônibus utiliza um sistema de vendas de passagens que fornece a imagem de todos os assentos do ônibus, diferenciando os assentos já vendidos, por uma cor mais escura, dos assentos ainda disponíveis. A empresa monitora, permanentemente, o número de assentos já vendidos e compara-o com o número total de assentos do ônibus para avaliar a necessidade de alocação de veículos extras.

Na imagem tem-se a informação dos assentos já vendidos e dos ainda disponíveis em um determinado instante.

A razão entre o número de assentos já vendidos e o total de assentos desse ônibus, no instante considerado na imagem, é:

A) 16/42

B) 16/26

C) 26/42

D) 42/26

E) 42/16

Questão: 12

(Enem 2013) Em um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas.

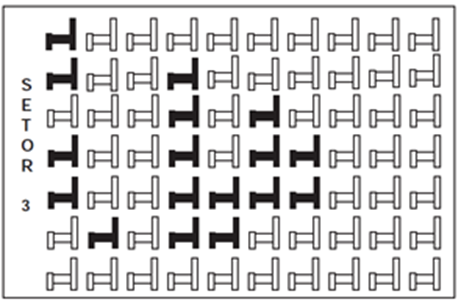
A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é

A) 17/70.

B) 17/53.

C) 53/70.

D) 53/17.

E) 70/17.

Respostas

Questão: 1

Alternativa C

Se no primeiro momento foram consumidos $\frac{3}{5}$ do bolo, então restaram $\frac{2}{5}$, pois 5 – 3 = 2. Agora, calculando $\frac{1}{2}$ de $\frac{2}{5}$:

$\frac{2}{5}\cdot\frac{1}{2}=\frac{2}{10}$ 

Simplificando a fração:

$\frac{2^{:2}}{{10}_{:2}}=\frac{1}{5}$ 

Questão: 2

Alternativa E

Calculando a fração irredutível:

$\frac{{200}^{:50}}{{350}_{:50}}=\frac{4}{7}\ $ 

Questão: 3

Alternativa A

Sabemos que 2/5 mais 1/3 tiraram nota acima da média, e que havia 60 alunos na sala, logo o número de estudantes abaixo da média x pode ser calculado por:

$x=60-\frac{2}{5}\cdot60-\frac{1}{3}\cdot60$ 

$x=60-\frac{120}{5}-\frac{60}{3}$ 

$x=\ 60\ -\ 24\ -\ 20$ 

$x=16$ 

Então 16 estudantes ficaram abaixo da média.

Questão: 4

Alternativa D

I) $\frac{9}{5}$ é imprópria, pois o numerador é maior que o denominador.

II) $\frac{9}{3}$ é aparente, pois 9 : 3 é um número inteiro.

III) $\frac{1}{3}$ é própria, pois o numerador é menor que o denominador.

A ordem correta é imprópria, aparente e própria.

Questão: 5

Alternativa A

Sabemos que há 8 meninas no total de 24 alunos, logo a fração será:

$\frac{8}{24}$ 

Note que é necessário simplificar essa fração:

$\frac{8^{:8}}{{24}_:8}=\frac{1}{3}$

Questão: 6

Alternativa E

Calculando a soma de 1/3 com 2/5:

$\frac{1}{3}+\frac{2}{5}=\frac{5+6}{15}=\frac{11}{15}$ 

Calculando o total de eleitores que não votaram:

$1-\frac{11}{15}=\frac{15-11}{15}=\frac{4}{15}$ 

Questão: 7

Alternativa B

Calculando, temos que:

$1-\frac{1}{4}-\frac{2}{5}$ 

$\frac{20-5-8}{20}$ 

$\frac{7}{20}$ 

Questão: 8

Alternativa D

I – Toda fração imprópria é um número maior que 1. (verdadeira)

Como o numerador é maior que o denominador, então o resultado da divisão será maior que 1.

II – Toda fração própria é um número menor que 1. (verdadeira)

Como o numerador é menor que o denominador, então o resultado da divisão será menor que 1.

III – Toda fração aparente é um número inteiro (verdadeira)

A fração é aparente se a divisão for exata, ou seja, um número inteiro.

Questão: 9

Alternativa E

Dados:

• m: mulher
• h: homem

Sabemos que:

$(\frac{1}{4}h+\frac{2}{3}m):\ 2=\frac{h}{4}$

Então, temos que:

$\frac{1}{4}h+\frac{2}{3}m=\frac{h}{2}$ 

$\frac{2}{3}m=\frac{h}{2}-\frac{h}{4}$ 

$\frac{2}{3}m=\frac{2h-h}{4}$ 

$\frac{2}{3}m=\frac{h}{4}$ 

$2\cdot4\ m\ =\ 3h$ 

$8m\ =\ 3h$ 

$m=\frac{3}{8}h$ 

Queremos encontrar a razão entre o número de homens e o número total de funcionários. Sabemos que o número total de funcionários é a soma h + m, portanto:

$\frac{h}{h+m}$ 

Substituindo m pelo valor encontrado anteriormente:

$\frac{h}{h+\frac{3}{8}h}$ 

$\frac{h}{\frac{8h+3h}{8}}$ 

$\frac{h}{\frac{11h}{8}}$ 

$h\cdot\frac{8}{11h}$ 

$\frac{8h}{11h}$ 

$\frac{8}{11}$

Questão: 10

Alternativa B.

O marcador de consumo de combustível indica que foi gasto 1/4 do combustível, logo restam 3/4. Como no tanque cabem 50 litros e o automóvel faz 15 km/L, com um tanque é possível percorrer 50 · 15 = 750 km. Agora basta calcular 3/4 de 750:

$\frac{3}{4}\cdot750$ 

$\frac{2250}{4}$ 

$562,5$ 

Questão: 11

Alternativa A.

Sabemos que há um total de 16 assentos vendidos entre os 42 acentos, logo a fração desejada é 16/42.

Questão: 12

Alternativa A

Há 17 cadeiras ocupadas entre as 70 cadeiras do setor, logo a fração desejada é 17/70.