Exercícios sobre paralelogramo
Estes exercícios sobre paralelogramos testarão seus conhecimentos sobre as propriedades dessa figura geométrica.
Perguntas
Questão: 1
Calcule a área de um paralelogramo que possui base igual a 15 centímetros e altura igual a 25 centímetros.
Questão: 2
Calcule a área de um quadrado de lado x – 2.
Questão: 3
(UFAM/2015) O piso de uma sala possui a forma de um paralelogramo como na figura a seguir.
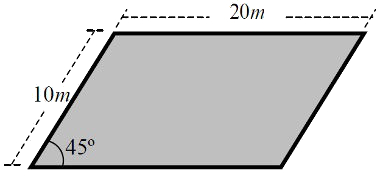
A área desse piso, em metros quadrados, mede:
OBS.: Considere √2 = 1,41
a) 0,141
b) 1, 41
c) 14,1
d) 141
e) 1410
Questão: 4
(UNEMAT/2015) Na figura plana abaixo, ABCD é um paralelogramo; ABDE, um retângulo de área 24 cm2 e D é um ponto do segmento EC.
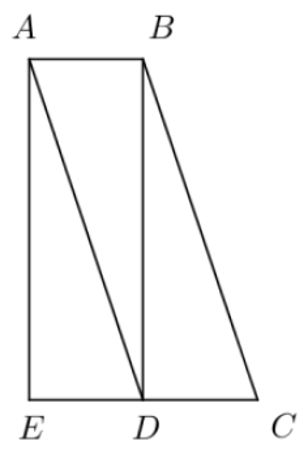
Qual é a área da figura ABCE ?
a) 36 cm2.
b) 48 cm2.
c) 52 cm2.
d) 44 cm2.
e) 30 cm2.
Respostas
Questão: 1
Para calcular a área do paralelogramo, ignora-se o valor de seu lado e considera-se apenas o valor de sua base e altura.
A fórmula da área do paralelogramo é: A = b·h, em que b é a base e h é a altura. Substituindo os valores na fórmula, teremos:
A = b·h
A = 15·25
A = 375 cm2
Questão: 2
A área do quadrado pode ser obtida da mesma forma que a área do paralelogramo, afinal, o quadrado também é um paralelogramo.
A = b·h
Porém, como o quadrado possui todos os lados iguais, substituindo o lado l do quadrado na fórmula acima, teremos:
A = l·l = l2
O quadrado que possui lado = x – 2 terá a área:
A = (x – 2)2
A = x2 – 4x + 4
Questão: 3
A altura desse paralelogramo pode ser obtida por meio do seno de 45°. Observe a figura:
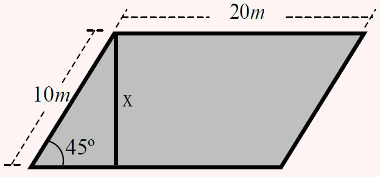
Sen45° = x
10
√2 = x
2 10
2x = 10√2
x = 10√2
2
x = 5√2
Resta apenas calcular a área do paralelogramo pela fórmula: A = base·altura
A = 20·5√2
A = 100√2
A = 100·1,41
A = 141 m2
Letra D.
Questão: 4
Como ABCD e ABDE são paralelogramos, além de lados opostos paralelos, eles possuem lados opostos congruentes. Como esses paralelogramos compartilham o lado AB, então: AB = ED e AB = DC. Dessa forma, necessariamente, ED = DC e D é o ponto médio de EC.
Observe que os lados AE e BD são congruentes porque ABDE é um paralelogramo. Já os lados AD e BC são congruentes porque ABCD também é um paralelogramo.
Considerando os triângulos AED, ABD e BCD, nota-se que, pelo caso LLL de congruência de triângulos, eles são congruentes. Escrevemos:
ADE = ABD = ACD (I)
Sendo os três triângulos congruentes, suas áreas também são congruentes.
Como a área de ABDE é 24 cm2, a área do triângulo ADE é:
ADE = ABDE
2
ADE = 24
2
ADE = 12 cm2
Dessa forma, observando a cadeia de igualdades (I), as áreas dos triângulos ABD e ACD também medem 12 cm2. Portanto, a área total da figura é dada pela soma das áreas desses três triângulos:
A = ADE +ABD + ACD
A = 12 + 12 + 12
A = 36 cm2
Letra A.
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-paralelogramo.htm