Perguntas

Questão: 1

Um ciclista vai sair do ponto A, ir até o ponto C e posteriormente vai ao ponto B, como mostrado no triângulo a seguir:

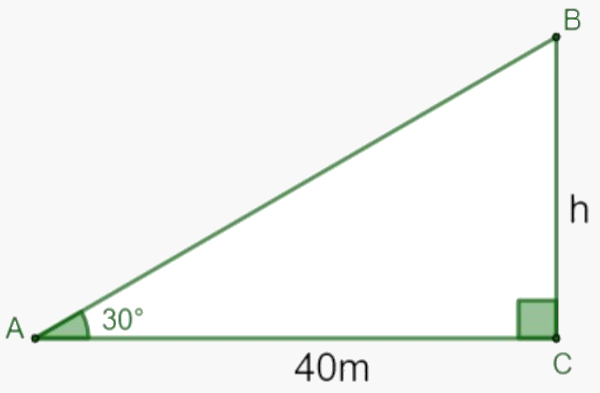
Qual será a distância percorrida pelo ciclista? (use $\sqrt{3} = 1,7$)

A) 62,7

B) 61,7

C) 60,4

D) 59,4

E) 58,7

Questão: 2

No triângulo a seguir, podemos identificar o ângulo notável de 45º.

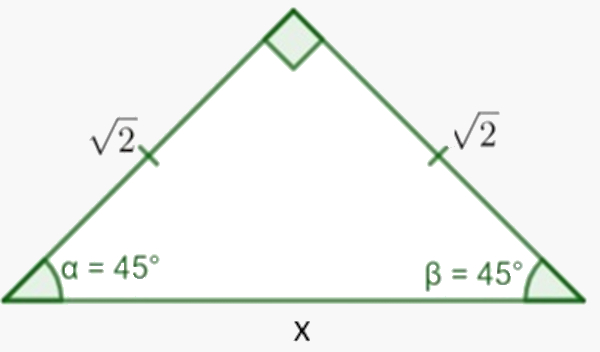
Analisando a imagem, podemos aficar que o valor de x é:

A) 1

B) 2

C) 3

D) 4

E) 5

Questão: 3

Em um terreno, um engenheiro deseja instalar uma rampa de acesso para um pequeno depósito elevado. A rampa será representada por um triângulo retângulo, cuja hipotenusa mede 5 metros e forma um ângulo de 30º com o solo. Qual será a altura aproximada do depósito em relação ao solo?

A) 5,0 m

B) 4,5 m

C) 4,0 m

D) 3,5 m

E) 3,0 m

F) 2,5 m

Questão: 4

Uma escada de 8 metros está apoiada em uma parede e forma um ângulo de 60° com o solo. Qual é a altura aproximada do topo da escada em relação ao chão?

A) 2 m

B) 4 m

C) 5 m

D) $4\sqrt{3}$ m

E) $6\sqrt{3}$ m

Questão: 5

Um avião inicia sua decolagem formando um ângulo de 30° com o solo. Se, após percorrer 500 metros, ele atingir uma altura de h metros, qual o valor de h?

A) 100 m

B) 150 m

C) 200 m

D) 250 m

E) 300 m

Questão: 6

Um barco parte de um porto e segue em linha reta em direção ao mar, formando um ângulo de 45° com a linha do horizonte. Se o barco percorreu 100 km, qual foi a distância horizontal percorrida?

A) $50\sqrt{2}$ km

B) $100\sqrt{2}$ km

C) 70 km

D) 90 km

E) 110 km

Questão: 7

Um foguete é lançado verticalmente, mas um observador está a 500 metros de distância do ponto de lançamento. Se o ângulo de elevação do observador até o foguete for de 45°, qual é a altura do foguete nesse momento?

A) 250 m

B) 400 m

C) 450 m

D) 500 m

E) 550 m

Questão: 8

Sobre os ângulos notáveis, julgue as afirmativas a seguir:

I. O valor de seno de 30º é igual ao valor do cosseno de 60º.

II. O valor da tangente de 45º é igual ao valor do cosseno de 45º.

III. O valor do seno de 60º é igual ao valor do cosseno de 60º.

Marque a alternativa correta:

A) Somente a afirmativa I é verdadeira.

B) Somente a afirmativa II é verdadeira.

C) Somente a afirmativa III é verdadeira.

D) Nenhuma das afirmativas é verdadeira.

Questão: 9

(Enem) Para decorar um cilindro circular reto, será usada uma faixa retangular de papel transparente, na qual está desenhada em negrito uma diagonal que forma 30° com a borda inferior. O raio da base do cilindro mede $\frac{6}{\pi}$cm, e, ao enrolar a faixa, obtém-se uma linha em formato de hélice, como na figura.

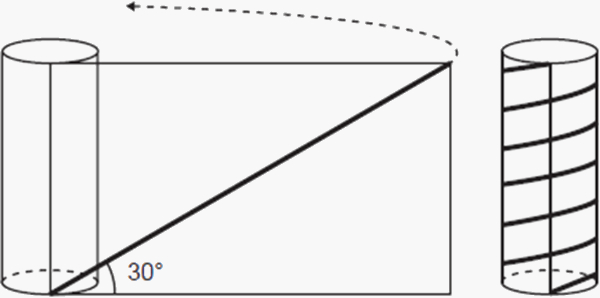
O valor da medida da altura do cilindro, em centímetro, é:

A) $36\sqrt{3}$

B) $24\sqrt{3}$

C) $4\sqrt{3}$

D) 36

E) 72

Questão: 10

(Enem)

Um balão atmosférico, lançado em Bauru (343 quilômetros a noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.

Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.

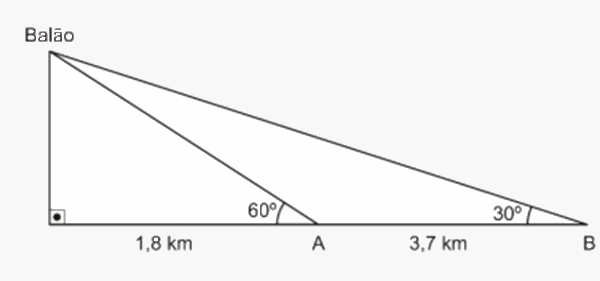
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°. Qual a altura aproximada em que se encontrava o balão?

A) 1,8 km

B) 1,9 km

C) 3,1 km

D) 3,7 km

E) 5,5 km

Questão: 11

(IFG) Teodolito é um instrumento de precisão para medir ângulos horizontais e ângulos verticais, utilizado em trabalhos de construção. Uma empresa foi contratada para pintar um edifício de quatro andares. Para descobrir a área total a ser pintada, ela precisa descobrir a altura do edifício. Uma pessoa posiciona o instrumento a 1,65 metros de altura, encontrando um ângulo de 30°, conforme mostra a figura. Supondo que o teodolito esteja distante $13\sqrt{3}$ metros do edifício, qual a altura, em metros, do prédio a ser pintado?

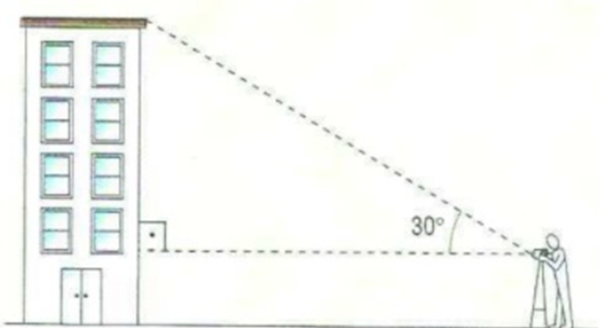
A) 11,65

B) 12,65

C) 13,65

D) 14,65

E) 15,65

Questão: 12

(Enem) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km, a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.

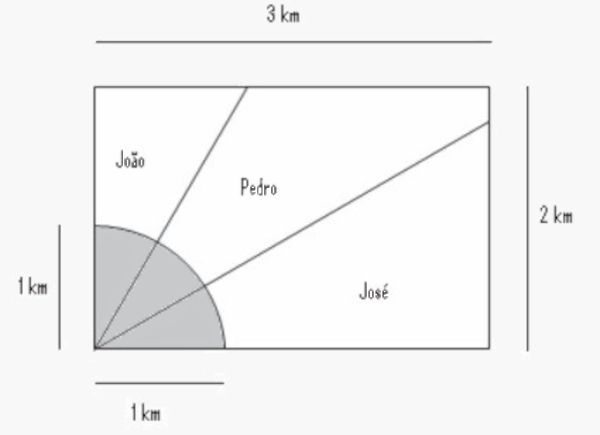
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a:

(Considere ${\sqrt{3}}/{3}$ = 0,58)

A) 50%

B) 43%

C) 37%

D) 33%

E) 19%

Respostas

Questão: 1

 Alternativa A.

Calculando o valor de h, temos que:

$tg 30^\circ = \frac{\text{CO}}{\text{CA}}$

$tg 30^\circ = \frac{h}{40}$

$\frac{\sqrt{3}}{3} = \frac{h}{40}$

 $\frac{1,7}{3} = \frac{h}{40}$

$3h=40 \cdot 1,7$

$3h=68$

$h = \frac{68}{3}$

$h=22,7$

Então, somando a distância de A até B, temos que:

$D = 22,7 + 40 = 62,7$  

Questão: 2

 Alternativa B.

Podemos aplicar tanto o seno quanto o cosseno para descobrir o valor de x, então temos que:

$sen 45^\circ = \frac{\text{CO}}{\text{hip}}$

$\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{x}$

$\sqrt{2} x = 2\sqrt{2}$

$x=2$ 

Questão: 3

 Alternativa E.

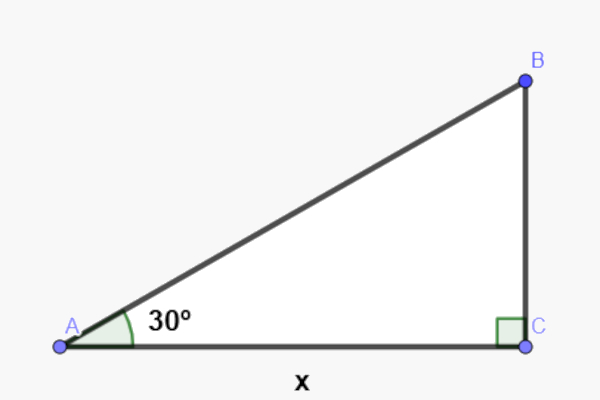
Primeiro representaremos a situação por meio de imagem:

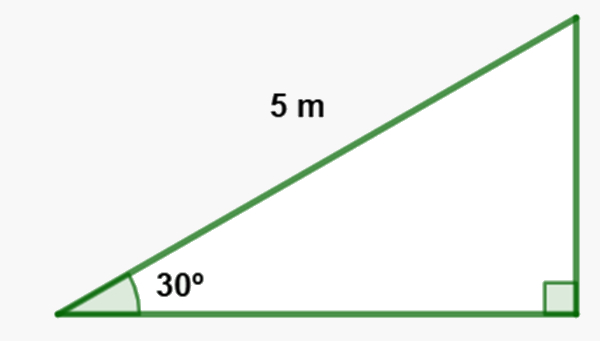
Agora aplicaremos o seno para encontrar a altura da rampa:

$sen 30^\circ = \frac{x}{5}$

$\frac{1}{2} = \frac{x}{5}$

$2x=5$

$x = \frac{5}{2}$

$x=2,5$ 

Questão: 4

 Alternativa C. 

Primeiro vamos ilustrar a situação:

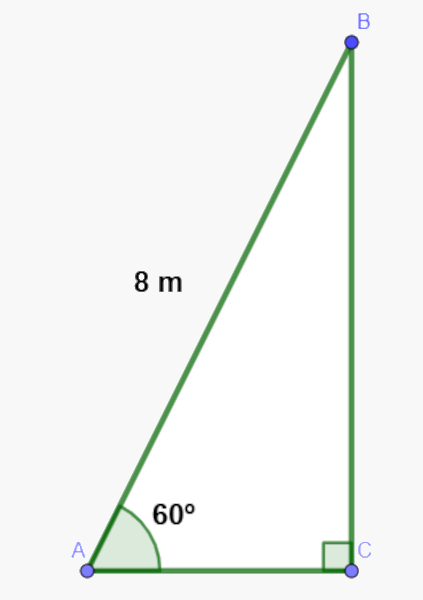
Agora aplicando seno para encontrar BC, temos:

$sen 60^\circ = \frac{\overline{BC}}{8}$

$\frac{\sqrt{3}}{2} = \frac{\overline{BC}}{8}$

$2\overline{BC} = 8\sqrt{3}$

$\overline{BC} = \frac{8\sqrt{3}}{2}$

$\overline{BC} = 4\sqrt{3}$  

Questão: 5

 Alternativa D.

Primeiro faremos a representação da situação em um triângulo:

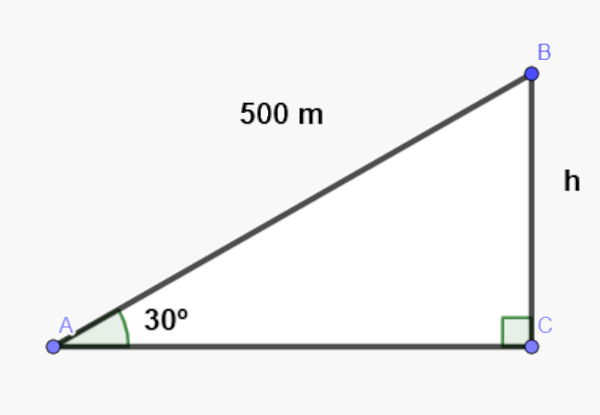
Aplicando seno de 30º, temos que:

$sen 30^\circ = \frac{h}{500}$

$\frac{1}{2} = \frac{h}{500}$

$2h=500$

$h = \frac{500}{2}$

$h=250$

Então a altura será de 250 metros. 

Questão: 6

 Alternativa A.

Seja d a distância horizontal, sabendo que ele percorreu 100 km, temos que é a hipotenusa do triângulo:

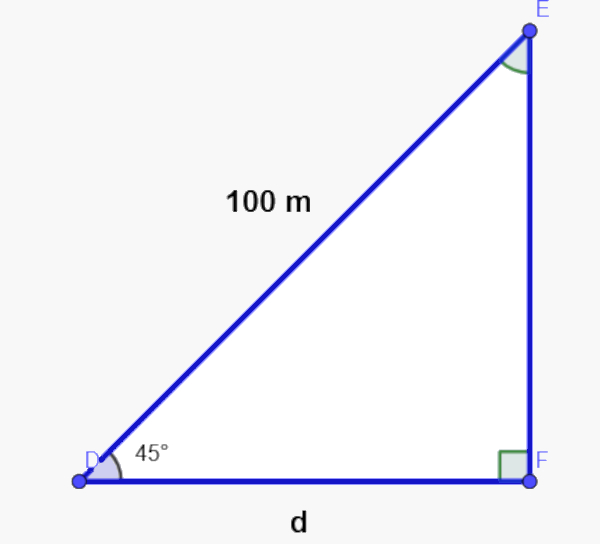
Aplicando cosseno de 45°, temos que:

$\cos 45^\circ = \frac{d}{100}$

$\frac{\sqrt{2}}{2} = \frac{d}{100}$

$2d = 100\sqrt{2}$

$d = \frac{100\sqrt{2}}{2}$

$d=50√2$ 

Questão: 7

Alternativa D.

Sabemos que a distância do observador até o foguete (cateto adjacente) é de 500 m.

O ângulo é de 45º, então, para encontrar a altura h, temos que:

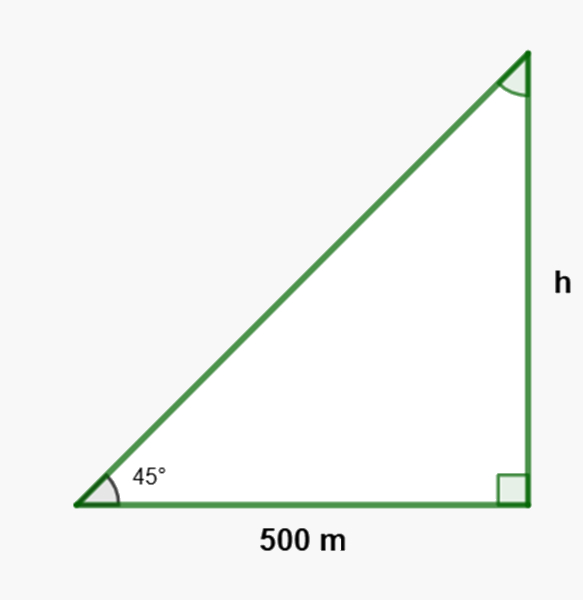
Aplicando tangente:

$\tan 45^\circ = \frac{h}{500}$

$1 = \frac{h}{500}$

$h=500 \cdot 1$

$h=500$

Questão: 8

Alternativa A

I. O valor de seno de 30º é igual ao valor do cosseno de 60º. (correta)

Sabemos que: $sen30^\circ = \cos 60^\circ = \frac{1}{2}$

II. O valor da tangente de 45º é igual ao valor do cosseno de 45º. (incorreta)

A tangente de 45º é igual a 1, já o cosseno de 45º é igual a $\frac{\sqrt{2}}{2}$.

III. O valor do seno de 60º é igual ao valor do cosseno de 60º. (incorreta)

O valor do seno de 60º é $\frac{\sqrt{3}}{2}$, já o cosseno de 60º é $\frac{{1}}{2}$.

Questão: 9

Alternativa B.

Primeiro, veja a representação do triângulo:

Sabemos que a medida de x é dada pela multiplicação de 6 vezes o comprimento da circunferência de raio $\frac{6}{\pi}$, ou seja:

$x = 6 \cdot 2\pi \cdot \frac{6}{\pi} = 72$

Agora, para achar BC, basta aplicar a tangente de 30º:

$tg 30^\circ = \frac{{BC}}{72}$

$\frac{\sqrt{3}}{3} = \frac{{BC}}{72}$

${BC} = 72 \cdot \frac{\sqrt{3}}{3}$

${BC} = 24\sqrt{3}$

Questão: 10

Alternativa C.

Aplicando tangente de 60º, temos que:

$tg 60^\circ = \frac{h}{1,8}$

$\sqrt{3} = \frac{h}{1,8}$

$h = 1,8 \cdot \sqrt{3}$

$h=1,8 \cdot 1,7$

$h=3,06$

Logo, a altura aproximada é de 3,1 km.

Questão: 11

Alternativa D.

Aplicando tangente de 30º, temos que:

$tg 30^\circ = \frac{\text{CO}}{\text{CA}}$

$\frac{\sqrt{3}}{3} = \frac{x}{13\sqrt{3}}$

$3x = 13\sqrt{3} \cdot \sqrt{3}$

$3x = 13 \cdot \sqrt{3^2}$

$3x=13 \cdot 3$

$\frac{3}{3} x = 13$

$x=13$

Somando a altura do instrumento:

$13+1,65 = 14,65 m$

Questão: 12

 Alternativa E.

Sabemos que o ângulo reto foi dividido em 3 partes iguais, então o ângulo representado pela região de extração de ouro é de 30º. A altura do retângulo é de 2 km do terreno, então, vamos calcular o cateto oposto ao ângulo utilizando a tangente.

$\tan 30^\circ = \frac{\text{CO}}{\text{CA}}$

$\frac{\sqrt{3}}{3} = \frac{x}{2}$

$0,58 = \frac{x}{2}$

$0,58 \cdot 2 = x$

$x=1,16$

Então, a área do terreno do João será:

$A = \frac{2 \cdot 1,16}{2}$

$A=1,16$

Se a área total é de 2 ⋅ 3 = 6, então temos que:

$1,16 \div 6 = 0,9 = 19\%$