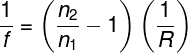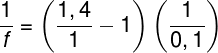Exercícios sobre a equação do fabricante de lentes
Esta lista de exercícios aborda a equação do fabricante de lentes, também conhecida como Equação de Halley, usada para definir o foco e vergência das lentes esféricas.
Perguntas
Questão: 1
Uma lente esférica e delgada apresenta distância focal de - 20 cm. É correto dizer que essa lente é _________ e sua vergência é de ____ di.
a) côncava, -5
b) convexa, 5
c) divergente, - 0,05
d) esférica, - 20
e) convergente, 5
Questão: 2
Uma lente plano-convexa imersa no ar (n = 1,0) apresenta índice de refração de 1,4 e raio de curvatura igual a 10 cm. Assinale, entre as alternativas a seguir, aquela que corresponde à distância focal dessa lente.
a) 25 m-1
b) 0,25 m-1
c) 0,5 m-1
d) 0,05 m-1
e) 0,4 m-1
Questão: 3
Uma lente delgada e côncava, cujo índice de refração absoluto é igual a 1,3, quando imersa em um líquido cujo índice de refração absoluto é de 1,5:
a) continuará divergindo os raios de luz incidentes sobre sua superfície.
b) passará a refletir a luz incidente sobre sua superfície.
c) será invisível dentro do líquido, já que a luz que se propaga tanto nela quanto no vidro apresenta a mesma velocidade.
d) passará a ser divergente, pois estará imersa em um líquido cujo índice de refração é maior que o seu.
e) passará a ser convergente, pois estará imersa em um líquido cujo índice de refração é maior que o seu.
Questão: 4
(Fuvest) Na formação das imagens na retina da vista humana normal, o cristalino funciona como uma lente:
a) convergente, formando imagens reais, diretas e diminuídas;
b) divergente, formando imagens reais, diretas e diminuídas;
c) convergente, formando imagens reais, invertidas e diminuídas;
d) divergente, formando imagens virtuais, diretas e ampliadas;
e) convergente, formando imagens virtuais, invertidas e diminuídas.
Respostas
Questão: 1
Letra A
Para calcularmos a vergência de uma lente, usamos a seguinte equação:
Sendo f o foco da lente em metros:
Temos que:
Logo:
Portanto, a vergência da lente é de – 5 di. O sinal negativo indica que a lente só conjuga imagens virtuais, sendo, portanto, côncava.
Questão: 2
Letra B
A equação do fabricante de lentes com pelo menos uma das faces planas é dada por:
De acordo com os dados fornecidos pelo enunciado da questão e lembrando que o raio de curvatura deve ser dado em metros (10 cm = 0,1 m), temos que:
Fazendo os cálculos das frações:
Assim, temos que:
Por fim, calculamos o foco da lente:
Questão: 3
Letra E
Quando imersas em meios cujo índice de refração absoluto é maior que seus próprios índices de refração, as lentes esféricas mudam a direção de refração dos raios de luz porque a luz se propaga mais rápido dentro de seu material do que no meio externo. Portanto, as lentes côncavas, que são divergentes quando imersas no ar atmosférico, passam a ser convergentes se inseridas em um meio mais refringente.
Questão: 4
Letra C
O cristalino é uma estrutura gelatinosa que se assemelha a uma lente biconvexa. Ele é capaz de formar imagens invertidas e menores, conjugando-as sobre o nervo óptico em condições normais.
Portanto, essa estrutura converge a luz e projeta uma imagem real, invertida e diminuída.
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-fisica/exercicios-sobre-equacao-fabricante-lentes.htm