Perguntas

Questão: 1

(FPS) Um automóvel percorre uma rodovia com velocidade inicialmente constante igual a 80 km/h. O motorista do veículo avista um radar e reduz sua velocidade para 60 km/h, percorrendo nesse trajeto uma distância igual a 20 m. O módulo da desaceleração sofrida pelo automóvel nesse percurso foi de aproximadamente:

A) 5,4 m/s²

B) 7,5 m/s²

C) 2,5 m/s²

D) 11 m/s²

E) 15 m/s²

Questão: 2

(Unesp) Um foguete lançador de satélites, partindo do repouso, atinge a velocidade de 5400 km/h após 50 segundos. Supondo que esse foguete se desloque em trajetória retilínea, sua aceleração escalar média é de

A) 30 m/s².

B) 150 m/s².

C) 388 m/s².

D) 108 m/s².

E) 54 m/s².

Questão: 3

(Uern) Veja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.

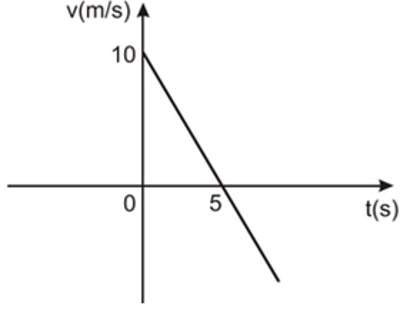
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é

A) 54 m.

B) 62 m.

C) 66 m.

D) 74 m.

Questão: 4

(FMTM) Um cientista, estudando a aceleração média de três diferentes carros, obteve os seguintes resultados:

O carro I variou sua velocidade de v para 2v em um intervalo de tempo igual a t.

O carro II variou sua velocidade de v para 3v em um intervalo de tempo igual a 2t.

O carro III variou sua velocidade de v para 5v em um intervalo de tempo igual a 5t.

Sendo, respectivamente, a1, a2 e a3 as acelerações dos carros I, II e III, pode-se afirmar que:

A) \(a_1=a_2=a_3\)

B) \(a_1>a_2>a_3\)

C) \(a_1<a_2<a_3\)

D) \(a_1=a_2>a_3\)

E) \(a_1=a_2<a_3\)

Questão: 5

Qual é a aceleração de um carro que estava inicialmente parado e atingiu uma velocidade de 70 m/s em 5 s?

A) \(13\ m/s^2\)

B) \(14\ m/s^2\)

C) \(15\ m/s^2\)

D) \(16\ m/s^2\)

E) \(17\ m/s^2\)

Questão: 6

O deslocamento angular final da roda de uma bicicleta é de 300 radianos. Sabendo que ela levou 60 segundos para completar esse deslocamento partindo do repouso, determine qual foi a aceleração aproximada sofrida pela roda.

A) \(0,16\ rad/s^2\)

B) \(0,20\ rad/s^2\)

C) \(0,24\ rad/s^2\)

D) \(0,28\ rad/s^2\)

E) \(0,32\ rad/s^2\)

Questão: 7

Considerando que a massa da Terra é de \(5,972\cdot 10^{24}\ kg\) e que o seu raio médio é 6.371 km, calcule a aceleração da gravidade da Terra sobre um corpo que está na superfície do planeta.

Dado: considere a constante de gravitação universal como \(6,67\cdot 10^{-11}\ N.m^2/kg^2\).

A) \(8,69\ m/s^2 \)

B) \(9,78\ m/s^2 \)

C) \(9,80\ m/s^2 \)

D) \(9,98\ m/s^2 \)

E) \(10,0\ m/s^2 \)

Questão: 8

Qual foi a aceleração angular média da roda de um motociclista que se movia com velocidade angular de 1,2 rad/s durante 3 segundos?

A) \(0,1\ rad/s^2\)

B) \(0,2\ rad/s^2\)

C) \(0,3\ rad/s^2\)

D) \(0,4\ rad/s^2\)

E) \(0,5\ rad/s^2\)

Questão: 9

Dentre as opções abaixo, qual não se trata de um tipo de aceleração?

A) Aceleração angular.

B) Aceleração centrípeta.

C) Aceleração da gravidade.

D) Aceleração tangencial.

E) Aceleração elástica.

Questão: 10

Uma pessoa corre com uma velocidade de 14,4 km/h ao redor de uma praça circular com 200 metros de raio. A partir dessas informações, qual a aceleração centrípeta do corredor?

A) \(0,16\ m/s^2\)

B) \(0,24\ m/s^2\)

C) \(0,32\ m/s^2\)

D) \(0,40\ m/s^2\)

E) \(0,48\ m/s^2\)

Questão: 11

Sabendo que o raio médio do planeta Marte é \(3,4\cdot 10^6\ m\) e a sua massa é de \(6,4\cdot 10^{23}\ kg\), calcule qual a aceleração da gravidade sofrida por um corpo que está distante 10.000 metros da superfície de Marte.

Dados: \(G = 6,67\cdot 10^{-11}\ N.m^2/kg^2\).

A) \(0,82\ m/s^2 \)

B) \(1,69\ m/s^2 \)

C) \(2,47\ m/s^2 \)

D) \(3,68\ m/s^2 \)

E) \(4,25\ m/s^2 \)

Questão: 12

Quais das alternativas apresentam as unidades de medida correspondentes às grandezas físicas estudadas na aceleração?

I. A aceleração é medida em metros por segundo.

II. A velocidade é medida em metros por segundo.

III. O tempo é medido em metros.

IV. A distância é medida em metros.

V. A altura é medida em metros por segundo ao quadrado.

A) Alternativas I e II.

B) Alternativas III e IV.

C) Alternativas I e V.

D) Alternativas II e III.

E) Alternativas II e IV.

Respostas

Questão: 1

Alternativa A.

Primeiramente, converteremos as velocidades de km/h para m/s:

\(\frac{80}{3,6}≅22,22\ m/s\)

\(\frac{60}{3,6}≅16,66\ m/s\)

Calcularemos a desaceleração através da fórmula de Torricelli:

\(v_f^2=v_i^2+2\cdot a\cdot ∆x\)

\(16,66^2=22,22^2+2\cdot a\cdot 20\)

\(277,77=493,82+40\cdot a\)

\(277,77-493,82≅40\cdot a\)

\(-216,05≅40\cdot a\)

\(a≅-\frac{216,05}{40}\)

\(a≅-5,40\ m/s^2 \)

Questão: 2

Alternativa A.

Primeiramente, converteremos a velocidade de km/h para m/s:

\(\frac{5400\ km/h}{3,6}=1500\ m/s\)

Calcularemos a aceleração média através da sua fórmula:

\(a_m=\frac{∆v}{∆t}\)

\(a_m=\frac{1500}{50}\)

\(a_m=30\ m/s^2 \)

Questão: 3

Alternativa B.

Primeiramente, calcularemos a aceleração desse corpo, através da fórmula da aceleração média:

\(a_m=\frac{∆v}{∆t}\)

\(a_m=\frac{v_f-v_i}{t_f-t_i}\)

\(a_m=\frac{0-10}{5-0}\)

\(a_m=-\frac{10}5\)

\(a_m=-2\ m/s^2\)

Então, calcularemos a distância final através da equação da função horária da posição no movimento retilíneo uniformemente variado:

\(x_f=x_i+v_i\cdot t+\frac{a\cdot t^2}2\)

\(x_f=46+10\cdot 8+\frac{-2\cdot 8^2}2\)

\(x_f=46+80+\frac{-2\cdot 64}2\)

\(x_f=46+80-64\)

\(x_f=62\ m\)

Questão: 4

Alternativa D.

Calcularemos a aceleração média de cada um dos veículos, através da sua fórmula:

\(a_m=\frac{∆v}{∆t}\)

\(a_m=\frac{v_f-v_i}{t_f-t_i}\)

• Carro 1:

\(a_1=\frac{∆v}{∆t}\)

\(a_1=\frac{v_f-v_i}{t_f-t_i}\)

\(a_1=\frac{2v-v}t\)

\(a_1=\frac{v}t\)

• Carro 2:

\(a_2=\frac{∆v}{∆t}\)

\(a_2=\frac{v_f-v_i}{t_f-t_i}\)

\(a_2=\frac{3v-v}{2t}\)

\(a_2=\frac{2v}{2t}\)

\(a_2=\frac{v}t\)

• Carro 3:

\(a_3=\frac{∆v}{∆t}\)

\(a_3=\frac{v_f-v_i}{t_f-t_i}\)

\(a_3=\frac{5v-v}{5t}\)

\(a_3=\frac{4v}{5t}\)

\(a_3=0,8\cdot \frac{v}t\)

Então, \(a_1=a_2>a_3\)

Questão: 5

Alternativa B.

Calcularemos a aceleração do carro através da equação da função horária da velocidade no movimento retilíneo uniformemente variado:

\(v_f=v_i+a\cdot t\)

\(70=0+a\cdot 5\)

\(70=a\cdot 5\)

\(\frac{70}5=a\)

\(14\ m/s^2=a\)

Questão: 6

Alternativa A.

Calcularemos a aceleração através da equação da função horária da posição no movimento circular uniformemente variado (MCUV):

\(φ_f=φ_i+ω_i\cdot t+\frac{α\cdot t^2}2\)

Como ele partiu do repouso, tanto a sua velocidade angular quanto deslocamentos iniciais serão nulos:

\(300=0+0\cdot 60+\frac{α\cdot 60^2}2\)

\(300=\frac{α\cdot 3600}2\)

\(300=α\cdot 1800\)

\(α=\frac{300}{1800}\)

\(α≅0,16\ rad/s^2\)

Questão: 7

Alternativa C.

Primeiramente, converteremos o raio médio de quilômetros para metros:

\(6.371\ km=6371000\ m=6,371\cdot 10^6\ m\)

Calcularemos a aceleração da gravidade da Terra sobre um corpo que está na superfície do planeta através da fórmula da aceleração da gravidade na superfície do planeta ou um corpo celeste:

\(g=\frac{G\cdot m}{r^2 }\)

\(g=\frac{6,7\cdot 10^{-11}\cdot 5,972\cdot 10^{24}}{(6,371\cdot 10^6)^2} \)

\(g=\frac{40,0124\cdot 10^{-11+24}}{40,589641\cdot 10^{12}}\)

\(g=\frac{40,0124\cdot 10^{13}}{40,589641\cdot 10^{12}}\)

\(g=0,985778613\cdot 10^{13-12}\)

\(g=0,985778613\cdot 10^1\)

\(g=9,85778613\)

\(g≈9,8\ m/s^2 \)

Questão: 8

Alternativa C.

Calcularemos a aceleração angular média através da sua fórmula:

\(α_m=\frac{∆ω}t\)

\(α_m=\frac{1,2}4\)

\(α_m=0,3\ rad/s^2\)

Questão: 9

Alternativa E.

Existem diversos tipos de aceleração, como a aceleração angular, a aceleração centrípeta, a aceleração das cargas, a aceleração da gravidade, a aceleração média e a aceleração tangencial, mas a aceleração elástica não é um desses tipos.

Questão: 10

Alternativa A.

Primeiramente, converteremos a velocidade de km/h para m/s:

\(\frac{14,4 km/h}{3,6}=4\ m/s\)

Calcularemos a aceleração centrípeta do corredor através da fórmula da aceleração centrípeta:

\(a_{CP}=\frac{v^2}R\)

\(a_{CP}=\frac{4^2}{100}\)

\(a_{CP}=\frac{16}{100}\)

\(a_{CP}=0,16\ m/s^2 \)

Questão: 11

Alternativa D.

Calcularemos a aceleração da gravidade para o corpo que está distante de Marte através da fórmula da aceleração da gravidade para corpos externos ao planeta ou um corpo celeste:

\(g=\frac{G\cdot m}{(r+h)^2}\)

\(g=\frac{6,7\cdot 10^{-11}\cdot 6,4\cdot 10^{23}}{(3,4\cdot 10^6+10\ 000)^2}\)

\(g=\frac{42,88\cdot 10^{12}}{(3\ 410\ 000)^2}\)

\(g=\frac{42,88\cdot 10^{12}}{11\ 628\ 100\ 000\ 000}\)

\(g≅3,68\cdot 10^{-12}\cdot 10^{12}\)

\(g≅3,68\ m/s^2 \)

Questão: 12

Alternativa E.

I. A aceleração é medida em metros por segundo. (incorreta)

A aceleração é medida em metros por segundo ao quadrado.

II. A velocidade é medida em metros por segundo. (correta)

III. O tempo é medido em metros. (incorreta)

O tempo é medido em segundos.

IV. A distância é medida em metros. (correta)

V. A altura é medida em metros por segundo ao quadrado. (incorreta)

A altura é medida em metros.