Perguntas

Questão: 1

Analise o polígono a seguir:

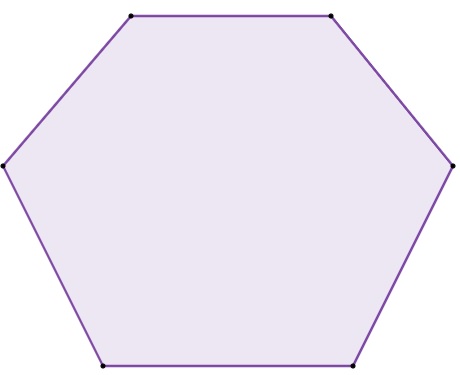
Esse polígono pode ser classificado como:

A) quadrilátero

B) pentágono

C) hexágono

D) heptágono

E) decágono

Questão: 2

Qual é o número de diagonais de um hexágono?

A) 7

B) 8

C) 9

D) 10

E) 11

Questão: 3

Qual é a área, em cm², de um hexágono regular que possui lados medindo $2\sqrt3$cm?

A) $2\sqrt3$

B) $9\sqrt3$

C) $18$

D) $18\sqrt3$

E) $36\sqrt3$

Questão: 4

A medida do apótema de um hexágono regular, com lados medindo $10\sqrt3$ cm, é igual a:

A) 12 cm

B) 15 cm

C) 16 cm

D) 17 cm

E) 20 cm

Questão: 5

Na reforma de uma praça, a prefeitura decidiu construir mesas com faces formadas por hexágonos. Para que a mesa seja considerada um hexágono regular, é necessário que a medida de cada ângulo interno seja igual a:

A) 120

B) 240

C) 360

D) 480

E) 720

Questão: 6

(USP) Uma das piscinas do Centro de Práticas Esportivas da USP tem o formato de três hexágonos regulares congruentes, justapostos, de modo que cada par de hexágonos tem um lado em comum, conforme representado na figura abaixo. A distância entre lados paralelos de cada hexágono é de 25 metros.

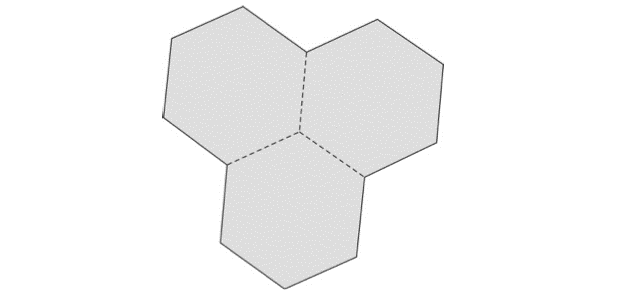
Assinale a alternativa que mais se aproxima da área da piscina.

A) 1600 m²

B) 1800 m²

C) 2000 m²

D) 2200 m²

E) 2400 m²

Questão: 7

Um terreno de 255 m² será cercado com arame. Para saber a quantidade necessária de arame, é necessário calcular o perímetro desse terreno. Sabendo que ele possui formato de um hexágono regular e utilizando $\sqrt3=1,7$, a medida do perímetro desse terreno é igual a:

A) $\sqrt3$

B) $6$

C) $10$

D) $6\sqrt{10}$

E) $10\sqrt6$

Questão: 8

Sobre o hexágono regular, qual é o valor da medida de um dos seus ângulos externos?

A) 120º

B) 80º

C) 60º

D) 50º

E) 40º

Questão: 9

(Aeronáutica) Dado um hexágono regular de 6 cm de lado, considere o seu apótema medindo a cm e o raio da circunferência a ele circunscrita medindo R cm. O valor de (R + a√3) é

A) 12

B) 15

C) 18

D) 25

Questão: 10

(UPE) A figura a seguir representa um hexágono regular de lado medindo 2 cm e um círculo cujo centro coincide com o centro do hexágono, e cujo diâmetro tem medida igual à medida do lado do hexágono.

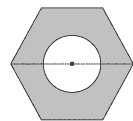
Considere $\pi=3\ e\ \sqrt3=1,7$

Nessas condições, quanto mede a área da superfície pintada?

A) 2,0 cm²

B) 3,0 cm²

C) 7,2 cm²

D) 8,0 cm²

E) 10,2 cm²

Questão: 11

Qual deve ser a medida do lado de um hexágono regular, sabendo que o seu apótema mede exatamente 6 cm?

A) $12$

B) $6$

C) $2\sqrt3$

D) $4\sqrt3$

E) $6\sqrt3$

Questão: 12

(Mackenzie) Um arame de 63 m de comprimento é cortado em duas partes e com elas constrói-se um triângulo e um hexágono regulares. Se a área do hexágono é 6 vezes a área do triângulo, podemos concluir que o lado desse triângulo mede:

A) 5 m

B) 7 m

C) 9 m

D) 11 m

E) 13 m

Respostas

Questão: 1

Alternativa C

Podemos perceber que o polígono possui 6 lados, então ele é um hexágono.

Questão: 2

Alternativa C

Para encontrar o número de diagonais de um hexágono, utilizamos a fórmula:

$d=\ \frac{n\cdot\left(n-3\right)}{2}$ 

Como o número de lados é 6, temos que:

$d=\frac{6\left(6-3\right)}{2}$ 

$d=\frac{6\cdot3}{2}$ 

$d=\frac{18}{2}$ 

$d=9$ 

Questão: 3

Alternativa D

Calculando a área do hexágono:

$A=\frac{3L^2\sqrt3}{2}$ 

 $A=\frac{3\cdot\left(2\sqrt3\right)^2\cdot\sqrt3}{2}$

$A=\frac{3\cdot4\cdot3\cdot\sqrt3}{2}$ 

$A=\frac{36\sqrt3}{2}$ 

$A=18\sqrt3$ 

Questão: 4

Alternativa B

Para calcular o apótema h do hexágono regular, utilizamos a fórmula: $h=\frac{L\sqrt3}{2}$

Então temos que:

$h=\frac{10\sqrt3\cdot\sqrt3}{2}$ 

$h=5\cdot\sqrt3\cdot\sqrt3$ 

$h=5\cdot3$ 

$h=15\ cm$ 

Questão: 5

Alternativa A

Primeiro calcularemos a medida das somas dos ângulos internos de um hexágono:

$S_i=\left(n-2\right)\cdot180$ 

$S_i=\left(6-2\right)\cdot180$ 

$S_i=4\cdot180$ 

$S_i=720$ 

O hexágono regular possui todos os ângulos com a mesma medida, então, dividindo 720 por 6, encontramos a medida de cada ângulo:

720 : 6 = 120°

Questão: 6

Alternativa A

Sabemos que a distância de um lado até o outro do hexágono é igual a 25, logo, a medida do apótema h desse hexágono é a metade de 25, ou seja, 12,5. Então temos que:

$h=\frac{l\sqrt3}{2}$ 

$12,5=\frac{l\sqrt3}{2}$ 

$12,5\cdot2=l\sqrt3$ 

$25=l\sqrt3$ 

$l=\frac{25}{\sqrt3}$ 

Agora podemos calcular a área do hexágono:

$A=3\cdot\frac{l^2\sqrt3}{2}$ 

$A=3\cdot\frac{\left(\frac{25}{\sqrt3}\right)^2\cdot\sqrt3}{2}$ 

$A=3\cdot\frac{\frac{625}{3}\cdot\sqrt3}{2}$ 

$A=\frac{625\sqrt3}{2}$ 

$A\approx531,25$ 

Como há 3 hexágonos, então, multiplicando a área por 3:

$A=3\cdot531,25=1593,75$ 

A área da piscina é de aproximadamente 1600 m².

Questão: 7

Alternativa D

Sabemos que a área A é igual a 255, então temos que:

$A=3\cdot\frac{l^2\sqrt3}{2}$ 

$255=3\cdot\frac{l^2\sqrt3}{2}$ 

$255\cdot2=3l^2\sqrt3$ 

$\frac{510}{3}=l^2\sqrt3$ 

$170=l^2\sqrt3$ 

Como $\sqrt3 = 1,7$:

$170=l^2\cdot1,7$ 

$\frac{170}{17}=l^2$ 

$l^2=10$ 

$l=\sqrt{10}$ 

Como ele possui 6 lados congruentes:

$P = 6\sqrt{10}$ 

Questão: 8

Alternativa C

A soma dos ângulos internos de um hexágono é sempre igual a 720º. Como esse hexágono é regular, cada ângulo interno mede 720 : 6 = 120°.

Como o ângulo externo é sempre suplementar ao ângulo interno, ou seja, a soma do externo com o interno é igual a 180°, temos que 180° – 120° = 60°, assim podemos concluir que ângulo externo mede 60°.

Questão: 9

Alternativa B

O raio da circunferência circunscrita no hexágono é igual ao lado do hexágono, logo, R = 6 cm. Agora calcularemos o apótema desse hexágono.

$a=\frac{l\sqrt3}{2}$ 

$a=\frac{6\sqrt3}{2}$ 

$a=3\sqrt3$

Então temos que:

$R+a\sqrt3$ 

$6+3\sqrt3\cdot\sqrt3$ 

$6+3\cdot3$

$6+9$ 

$15$ 

Questão: 10

Alternativa C

Para calcular a área da superfície pintada, calculamos a diferença entre a área do hexágono $A_H$ e a área do círculo $A_c$ .

Temos que o lado do hexágono é igual a 2:

$A_H=3\cdot\frac{l^2\sqrt3}{2}$ 

$A_H=3\cdot\frac{2^2\cdot1,7}{2}$ 

$A_H=3\cdot2\cdot1,7$ 

$A_H=6\cdot1,7$ 

$A_H=10,2$ 

Agora calculando a área do círculo, como o diâmetro mede 2 cm, então o seu raio é 1 cm.

$A_C=\pi r^2$ 

$A_C=3\cdot1^2$ 

$A_C=3$ 

Por fim, calculamos a diferença:

$A_H-A_C=10,2-3=7,2$ 

Questão: 11

Alternativa D

Sabemos que:

$a=\frac{l\sqrt3}{2}$ 

Então substituindo o valor do apótema, temos que:

$6=\frac{l\sqrt3}{2}$ 

$6\cdot2=l\sqrt3$ 

$12=l\sqrt3$ 

$\frac{12}{\sqrt3}=l$ 

$\frac{12}{\sqrt3}\cdot\frac{\sqrt3}{\sqrt3}=l$ 

$\frac{12\sqrt3}{3}=l$ 

$l=4\sqrt3$ 

Questão: 12

Alternativa B

Como a área do hexágono é igual a 6 vezes a área do triângulo equilátero, isso significa que os lados do hexágono são congruentes aos lados do triângulo equilátero, pois sabemos que um hexágono regular pode ser dividido em 6 triângulos equiláteros.

Sabemos que a soma dos lados do hexágono e do triângulo é igual a 63 m, então temos que:

6l + 3l = 63

9l = 63

l = 63 : 9

l = 7