Perguntas

Questão: 1

(Unipac) Uma prensa hidráulica possui pistões com diâmetros de 10 cm e 20 cm. Se uma força de 120 N atua sobre o pistão menor, pode-se afirmar que essa prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de:

a) 30 N

b) 60 N

c) 480 N

d) 240 N

e) 120 N

Questão: 2

(PUC-RS) No oceano a pressão hidrostática aumenta aproximadamente uma atmosfera a cada 10 m de profundidade. Um submarino encontra-se a 200 m de profundidade, e a pressão do ar no seu interior é de uma atmosfera. Nesse contexto, pode-se concluir que a diferença da pressão entre o interior e o exterior do submarino é, aproximadamente, de

a) 200 atm

b) 100 atm

c) 21 atm

d) 20 atm

e) 19 atm

Questão: 3

(Udesc) Certa quantidade de água é colocada em um tubo em forma de U, aberto nas extremidades. Em um dos ramos do tubo, adiciona-se um líquido de densidade maior que a da água, e ambos não se misturam.

Assinale a alternativa que representa corretamente a posição dos dois líquidos no tubo após o equilíbrio.

Questão: 4

(UFF-RJ) O sifão é um instrumento usado para a retirada de água de lugares de difícil acesso.

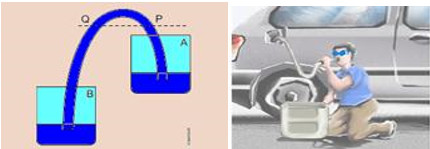
Como mostra a figura a seguir, seu funcionamento se baseia no fato de que, quando o tubo que liga os recipientes A e B está cheio, há uma diferença de pressão hidrostática entre os pontos P e Q, o que provoca um fluxo de água de A para B. Essa diferença de pressão depende da seguinte característica do nosso planeta:

a) pressão atmosférica.

b) aceleração da gravidade local.

c) temperatura da superfície.

d) densidade da atmosfera.

e) velocidade de rotação do planeta.

Questão: 5

Quando se aplica uma força de 300 N sobre o menor pistão de uma prensa hidráulica, com raio de 0,4 metros, ocorrerá uma força sobre o pistão maior, com raio de 0,8 metros, com valor de:

a) 300 N

b) 600 N

c) 900 N

d) 1200 N

e) 2400 N

Questão: 6

Calcule a variação de pressão sobre um mergulhador que está a uma profundidade de 0,5 metros, sabendo que a densidade da água é 1000 kg/m e a aceleração da gravidade é $10\ m/s^2$.

a) $3\cdot 10^3\ Pa$

b) $4\cdot 10^3\ Pa$

c) $5\cdot 10^3\ Pa$

d) $6\cdot 10^3\ Pa$

e) $7\cdot 10^3\ Pa$

Questão: 7

Calcule a altura atingida pela água quando ela é despejada em um recipiente em formato de U que contém óleo e que após o equilíbrio tem uma altura de 0,8 metros, sabendo que a densidade da água é $1000\ kg/m^3$ e do óleo é $800\ kg/m^3$.

a) 1,00 m

b) 0,32 m

c) 0,50 m

d) 0,80 m

e) 0,64 m

Questão: 8

Calcule a área do pistão maior de uma prensa hidraúlica que recebe uma força de 200 N, sabendo que sobre o pistão menor de $2\ m^2$ é aplicada uma força de 80 N.

a) $2\ m^2$

b) $3\ m^2$

c) $4\ m^2$

d) $5\ m^2$

e) $6\ m^2$

Questão: 9

Após seus estudos a respeito do Teorema de Stevin, determine quais das proposições abaixo são consideradas suas aplicações:

I) Princípio de Bernoulli.

II) Teorema de Arquimedes.

III) Vasos comunicantes.

IV) Teorema de Pascal.

a) Alternativas I e II.

b) Alternativas III e IV.

c) Alternativas I e III.

d) Alternativas II e IV.

e) Alternativas I e IV.

Questão: 10

Qual a profundidade máxima que um nadador pode alcançar sabendo que o seu pulmão suporta uma diferença de pressão de 0,08 atm? Considere que a densidade da água é 1000 kg/m e a aceleração da gravidade é $10\ m/s^2$.

a) 0,08106 m

b) 0,008106 m

c) 0,8106 m

d) 8,106 m

e) 81,06 m

Questão: 11

Calcule a densidade do líquido que é despejado em um recipiente contendo mercúrio, cuja densidade é $13,534\ g/m^3$, sabendo que o líquido está a uma altura de 30 cm e o mércurio, a 90 cm.

a) $40,602\ g/m^3$

b) $50,786\ g/m^3$

c) $60,902\ g/m^3$

d) $70,413\ g/m^3$

e) $80,258\ g/m^3$

Questão: 12

Quais proposições apresentam a unidade de medida correspondente à grandeza física estudada no teorema de Stevin?

I) A densidade é medida em $kg/m^3$.

II) A altura é medida em Pascal.

III) A pressão é medida em metros por segundo.

IV) A força é medida em Newton.

a) Alternativas I e II.

b) Alternativas III e IV.

c) Alternativas I e III.

d) Alternativas II e IV.

e) Alternativas I e IV.

Respostas

Questão: 1

Letra A.

Primeiramente, calcularemos o raio do pistão maior, por meio do seu diâmetro:

$r_1=\frac{d_1}2$

$r_1=\frac{20}2$

$r_1=10\ cm$

E o raio do pistão menor:

$r_2=\frac{d_2}2$

$r_2=\frac{10}2$

$r_2=5\ cm$

Depois, calcularemos a área do pistão maior:

$A_1=π\cdot r_1^2$

$A_1=π\cdot 10^2$

$A_1=100π\ cm^2$

E a área do pistão menor:

$A_2=π\cdot r_2^2$

$A_2=π\cdot 5^2$

$A_2=25π\ cm^2$

Por fim, substituiremos os dados na fórmula do teorema de Pascal:

$\frac{F_1}{A_1} =\frac{F_2}{A_2}$

$\frac{120}{100π}=\frac{F_2}{25π}$

$F_2=\frac{120\cdot 25π}{100π}$

$F_2=30\ N$

Questão: 2

Letra D.

De início, calcularemos a pressão externa usando o teorema de Stevin:

$∆p=p-p_o$

Lembrando que $p_o$ é a pressão atmosférica, p é a pressão absoluta, que nesse caso se trata da pressão externa $p_e$, e $∆p$ é a pressão manométrica, que nesse caso se trata da pressão hidrostática $p_h$.

$p_h=p_e-p_o$

$p_e=p_h+p_o$

De acordo com o enunciado, a cada 10 metros a pressão hidrostática aumenta 1 atm, então a uma profundidade de 200 metros, a pressão hidrostática é 20 atm e a pressão atmosférica é 1 atm. Assim, a pressão externa é:

$p_e=p_h+p_o$

$p_e=20+1$

$p_e=21\ atm$

Por fim, calcularemos a diferença de pressão no interior e no exterior do submarino, sabendo que a pressão interna é 1 atm:

$∆p=p_e-p_i$

$∆p=21-1$

$∆p=20\ atm$

Questão: 3

Letra D.

Ao se colocar líquidos a diferentes densidades em um recipiente em U, eles terão alturas diferentes, ainda que apresentem a mesma pressão. Como a densidade da água é menor que a densidade do líquido, a altura da água deve ser maior que a altura do líquido.

Questão: 4

Letra B.

Podemos analisar essa questão por meio da fórmula do teorema de Stevin:

$∆p=d\cdot g\cdot ∆h$

De acordo com o teorema, a variação de pressão hidrostática depende da densidade do líquido, da aceleração da gravidade local e da variação de altura.

Questão: 5

Letra D.

Inicialmente, calcularemos a área do pistão maior:

$A_1=π\cdot r_1^2$

$A_1=π\cdot 0,4^2$

$A_1= 0,16π\ m^2$

E a área do pistão menor:

$A_2=π\cdot r_2^2$

$A_2=π\cdot 0,8^2$

$A_2=0,64π\ m^2$

Por fim, substituiremos os dados na fórmula do teorema de Pascal:

$\frac{F_1}{A_1} =\frac{F_2}{A_2}$

$\frac{300}{0,16π}=\frac{F_2}{0,64π}$

$F_2=\frac{300\cdot 0,64π}{0,16π}$

$F_2=1200\ N$

Questão: 6

Letra C.

Calcularemos a variação de pressão sobre o mergulhador usando o teorema de Stevin:

$∆p=d\cdot g\cdot ∆h$

$∆p=1000\cdot 10\cdot 0,5$

$∆p=5000$

$∆p=5\cdot 10^3\ Pa$

Questão: 7

Letra E.

Calcularemos a altura atingida pela água por meio da fórmula do princípio dos vasos comunicantes:

$\frac{H_1}{H_2} =\frac{d_2}{d_1}$

$\frac{H_1}{0,8}=\frac{800}{1000}$

$H_1=\frac{0,8\cdot 800}{1000}$

$H_1=0,64\ m$

Questão: 8

Letra D.

Calcularemos a área do pistão maior, usando o teorema de Pascal:

$\frac{F_1}{A_1} =\frac{F_2}{A_2}$

$\frac{80}{2}=\frac{200}{A_2}$

$A_2=\frac{200\cdot 2}{80}$

$A_2=5\ m^2$

Questão: 9

Letra B. Os vasos comunicantes e o teorema de Pascal são aplicações do teorema de Stevin, já que ele propiciou o desenvolvimento deles.

Questão: 10

Letra C.

Primeiramente, transformaremos a pressão de atm para Pascal:

0,08 atm = 8106 Pa

Depois, calcularemos a profundidade máxima atingida pelo nadador por meio do teorema de Stevin:

$∆p=d\cdot g\cdot ∆h$

$8106=1000\cdot 10\cdot ∆h$

$∆h=\frac{8106}{1000\cdot 10}$

$∆h=0,8106\ m$

Questão: 11

Letra A.

De início, converteremos as alturas de centímetros para metros:

30 cm = 0,3 m

90 cm = 0,9 m

Depois, calcularemos a densidade do líquido usando a fórmula do princípio dos vasos comunicantes:

$\frac{H_1}{H_2} =\frac{d_2}{d_1}$

$\frac{0,3}{0,9}=\frac{13,534}{d_1}$

$d_1=\frac{13,534\cdot 0,9}{0,3}$

$d_1=40,602\ g/m^3$

Questão: 12

Letra E.

Abaixo, vemos a correção, em vermelho, das alternativas incorretas.

I) Correta.

II) Incorreta. A altura é medida em metros.

III) Incorreta. A pressão é medida em Pascal.

IV) Correta.