Exercícios sobre matriz simétrica
Teste seus conhecimentos por meio desta lista de exercícios sobre matriz simétrica, a matriz cuja sua transposta é ela mesma.
Perguntas
Questão: 1
Sabendo que a matriz A é simétrica, determine o valor de x.
A=[2x87]
A) 2
B) 8
C) 7
D) -2
E) -7
Questão: 2
Determine o valor de x e y sabendo que a matriz M é simétrica.
M=(3x−298479y+25)
A) x = 8 e y = 7
B) x = 6 e y = 9
C) x = 10 e y = 9
D) x = 10 e y = 5
E) x = 5 e y = 7
Questão: 3
Analise as afirmações abaixo e marque a alternativa correta.
I. Toda matriz simétrica é de ordem 2x2.
II. Toda matriz identidade é simétrica.
III. Toda matriz nula é uma matriz simétrica.
A) Apenas o item I é falso.
B) Todos os itens são verdadeiros.
C) Somente os itens I e II são verdadeiros.
D) Temos apenas um item verdadeiro.
E) Todos os itens são falsos.
Questão: 4
Considere que a matriz A é simétrica, de ordem 2x2, e obedece à lei de formação:
a={aij=sen(iπ), se i=1 aij=cos(iπ), se i≠1 e i=j
Determine a matriz B que satisfaz a equação matricial A+B = 0:
A) (1010)
B) (1001)
C) (100−1)
D) (000−1)
E) (0001)
Questão: 5
Determine o valor de a e b sabendo que a matriz A é simétrica.
A=(6a−b94469a+b9)
A) a = 4 e b = 7
B) a = 5 e b = 1
C) a = 1 e b = 6
D) a = 3 e b = 5
E) a = 5 e b = 7
Questão: 6
Sabendo que a matriz simétrica N de ordem 2x2 obedece à lei de formação a={a12=3 aij=2, se i=j, podemos afirmar que N é:
A) (3223)
B) (2233)
C) (2332)
D) (3322)
E) (3232)
Questão: 7
Sendo N=(23−12), M=(7882) e P=(5−175) matrizes de ordem 2x2, marque a alternativa verdadeira:
A) N é uma matriz simétrica.
B) M é uma matriz transposta de N.
C) M é matriz simétrica.
D) P é matriz simétrica.
E) N é matriz nula.
Questão: 8
A=(7yxy) e B=(7xy2) são matrizes de ordem 2x2. Sabendo que a matriz B é igual à matriz A e supondo que a matriz A seja matriz simétrica, determine os valores de x e y:
A) x = 7 e y = 2
B) x = 7 e y = 7
C) x = 2 e y = 2
D) x = 2 e y = 7
E) x = 1 e y = 6
Questão: 9
A=(689x4y969) é uma matriz simétrica. Determine a soma de todos os elementos da matriz oposta de A.
A) 65
B) -65
C) -51
D) 51
E) 34
Questão: 10
Sejam X e Y matrizes 2x2 satisfazendo a expressão X∙Y+Y∙X=0. Sabendo que X é matriz simétrica e Y é igual à transposta da matriz X, podemos afirmar que:
A) O determinante de X é 1.
B) O determinante de Y é 1.
C) X é matriz identidade.
D) Y é matriz identidade.
E) X e Y são matrizes nulas.
Questão: 11
Sobre a definição de matriz simétrica, classifique os itens abaixo em verdadeiros ou falsos.
I. Toda matriz nula é simétrica.
II. Toda matriz identidade é simétrica.
III. Toda matriz simétrica é uma matriz identidade.
IV. Toda matriz que é igual a sua transporta é uma matriz simétrica.
V. Existe matriz simétrica que não é uma matriz quadrada.
A) Dois itens verdadeiros.
B) Um item verdadeiro.
C) Quatro itens verdadeiros.
D) Três itens verdadeiros.
E) Todos os itens são verdadeiros.
Questão: 12
Observe as matrizes a seguir e julgue os itens.
M=(479846909)
B=(689845959)
C=(6−1984−1989)
I. A matriz M é simétrica.
II. A matriz B é simétrica.
III. A matriz C é simétrica.
IV. Nenhuma das matrizes acima é simétrica.
A) Dois itens verdadeiros.
B) Um item verdadeiro.
C) Quatro itens verdadeiros.
D) Três itens verdadeiros.
E) Todos os itens são verdadeiros.
Respostas
Questão: 1
Alternativa B.
Observe que o enunciado afirma que a matriz é simétrica, logo os elementos a12 e a21 devem ser iguais. Na figura abaixo isso é claro, e podemos concluir que x = 8.
A=[2x87]=[2a12a127]
Questão: 2
Alternativa D.
Como o enunciado nos traz que a matriz é uma matriz simétrica, primeiro analisaremos 4 termos dessa matriz em específico:
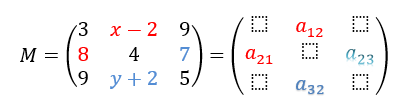
Analisando a matriz, temos que {a21=8a12=x−2 e {a32=y+2a23=7
Sabemos que M é matriz simétrica, então a12 = a21 e a32 = a23. Sendo assim, temos que:
x−2=8
x=8+2
x=10
Calculando o valor de y, temos que:
y+2=7
y=7−2
y=5
Então temos que x = 10 e y = 5.
Questão: 3
Alternativa D.
I. Toda matriz simétrica é de ordem 2x2. (falso)
Existem matrizes simétricas de qualquer ordem.
II. Toda matriz identidade é simétrica. (verdadeiro)
Como os elementos fora da diagonal principal são iguais a zero, não há possibilidade para ter aij≠aji.
III. Toda matriz nula é uma matriz simétrica. (falso)
Existem matrizes nulas que não são quadradas, condição necessária para serem simétricas.
Questão: 4
Alternativa D.
Vamos montar a matriz genérica com base nas informações do enunciado.
A=(a11a12a21a22)
a11=sen(1⋅π)=0
a12=sen(1⋅π)=0
a21 = 0 (da definição de matriz simétrica, pois a12 = a 21)
a22=cos(2⋅π)=1
A=(0001)
Pelo sistema de equação matricial, temos que B = -A:
B=(000−1)
Questão: 5
Alternativa B.
Analisaremos os termos em destaque:
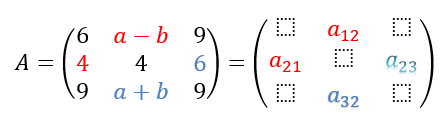
Temos que: {a21=4a12=a−be {a32=a+ba23=6
Ao afirmar que A é matriz simétrica, concluímos que a12=a21 e a32=a23. Sendo assim, temos que:
{a−b=4a+b=6
Efetuando a soma das duas linhas:
2a= 10
a=102
a=5
Logo a=5.
Substituindo esse valor na segunda linha do sistema:
a+b=6
5+b=6
b=1
Questão: 6
Alternativa C.
Vamos montar a matriz genérica com base nas informações do enunciado.
N=(a11a12a21a22)
a11=2
a22=2
a12=3
Como a matriz N é simétrica, temos que a12=a21=3.
N=(2332)
Questão: 7
Alternativa C.
A alternativa A é falsa, pois caso a matriz N fosse simétrica, os elementos -1 e 3 deveriam ser iguais.
A alternativa B é falsa. As matrizes M e N possuem elementos distintos. Numa matriz transposta o que muda é a ordem dos elementos e não seus valores.
A alternativa C é verdadeira. Os elementos a12=a21=8.
A alternativa D é falsa, pois caso a matriz N fosse simétrica, os elementos -1 e 7 deveriam ser iguais.
A alternativa E é falsa, pois a matriz possui elementos diferentes de zero.
Questão: 8
Alternativa C.
Pela definição de matriz simétrica, temos que A=(7yxy)=(7xyy)=(7xy2). Assim, concluímos que x = y = 2.
Questão: 9
Alternativa B.
Pela definição de matriz simétrica, temos que:
A=(689x4y969)=(6x98469y9)
A partir disso, concluímos que x = 8 e y = 6. Somando os termos dessa matriz e multiplicando por -1, obtemos −(6+8+9+8+4+6+9+6+9)=−65..
Questão: 10
Alternativa E.
Do fato de a matriz X ser simétrica temos X = Y, logo temos que X2+X2=2X2=0.
Escrevendo esse produto de forma genérica:
2(abbc)(abbc)=2(a2+b2ab+bcab+b2b2+c2)=(0000)
Do resultado acima concluímos que a = 0, e b = 0, e c = 0.
Logo, as matrizes X e Y são matrizes nulas.
Questão: 11
Alternativa A.
I. Toda matriz nula é simétrica. (falso)
Existem matrizes nulas que não são quadradas, logo não são simétricas.
II. Toda matriz identidade é simétrica. (verdadeiro)
Como os elementos fora da diagonal principal são iguais a zero, não há possibilidade de haver aij≠aji.
III. Toda matriz simétrica é uma matriz identidade. (falso)
Existem matrizes simétricas com elementos da diagonal principal diferentes de 1, logo não são simétricas.
IV. Toda matriz que é igual a sua transporta é uma matriz simétrica. (verdadeiro)
Essa é a definição de matriz simétrica.
V. Existe matriz simétrica que não é uma matriz quadrada. (falso)
É uma consequência que a matriz simétrica seja quadrada.
Questão: 12
Alternativa B.
I. A matriz M é simétrica. (falso)
M não é uma matriz simétrica, pois os números 7 e 8 são diferentes, além de 6 e 0 serem diferentes. Esses são os elementos que deveriam ser iguais.
II. A matriz B é simétrica. (verdadeiro)
Os elementos fora da diagonal principal são vistos como espelhados por ela.
III. A matriz C é simétrica. (falso)
C não é uma matriz simétrica, pois os números -1 e 8 são diferentes. Esses são os elementos que deveriam ser iguais.
IV. Nenhuma das matrizes acima é simétrica. (falso)
O item II ser verdadeiro torna esse item falso.
Fonte: Brasil Escola - https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-matriz-simetrica.htm