Exercícios sobre Divisão de Números Complexos
Para resolver estes exercícios sobre divisão de números complexos, é necessário aplicar a ideia de conjugado de um número complexo e a propriedade distributiva da multiplicação.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Determine o valor do quociente dos números complexos z1 e z2, sabendo que z1 = 2 – 3i e z2 = – 1 + 2i.
Representando esse quociente como fração, temos z1 como numerador e z2 como denominador. Para determinar o quociente, multiplicamos numerador e denominador pelo conjugado deste. Temos então:
z1 = 2 – 3i
z2 – 1 + 2iz1 = (2 – 3i ) . (– 1 – 2i)
z2 (– 1 + 2i) . (– 1 – 2i)z1 = – 2 + 3i – 4i + 6.i²
z2 (– 1)² – (2i)²z1 = – 2 + 3i – 4i – 6
z2 1 – (– 4)z1 = – 8 – i
z2 5Portanto, o quociente entre os complexos z1 e z2 é - 8 - i.
5 -
Questão 2
Escreva, na forma complexa z = a + bi, o número complexo:
z = (5 + 2i) . (2 – i)
3 + iPrimeiramente, aplicamos a propriedade distributiva da multiplicação no numerador da fração:
z = 10 + 4i – 5i – 2i²
3 + iz = 10 – i – 2.(– 1)
3 + iz = 10 – i + 2
3 + iz = 12 – i
3 + iPara realizar a divisão, vamos multiplicar as duas partes da fração pelo conjugado do denominador:
z = (12 – i).(3 – i)
(3 + i).(3 – i)z = 36 – 12i – 3i + i²
9 – i²z = 36 – 15i + (– 1)
9 – (– 1)z = 36 – 15i – 1
9 + 1z = 35 – 15i
10z = 7 – 3i
2Portanto, na forma complexa, temos z = 7/2 – 3i/2.
-
Questão 3
(Cefet – PR) A expressão
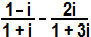, na qual i é a unidade imaginária, é igual a:Vamos separar a expressão, logo: A =
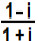e B =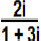 
. No fim da resolução, faremos A – B. Agora calculamos a divisão de números complexos que ocorre em A, multiplicando a fração pelo conjugado do denominador:A = 1 – i . 1 – i
1 + i 1 – iA = (1 – i)²
(1 + i).(1 – i)A = 1 – 2.i – 1
1 – (– 1)A = – 2.i
2A = – i
Agora que já encontramos o valor de A, vamos utilizar o mesmo processo para determinar o valor de B:
B = 2i . 1 – 3i
1 + 3i 1 – 3iB = 2i.(1 – 3i)
(1 + 3i).(1 – 3i)B = 2i + 6
1 – (– 9)B = 6 + 2i
10B = 3 + i
5Agora já podemos resolver a expressão:
A – B = – i – 3 + i
5A – B = – 5i – (3 + i)
5A – B = – 5i – 3 – i
5A – B = – 3 – 6i
5Portanto, a alternativa correta é a letra a.
-
Questão 4
(UFRS) A forma a + bi de z = 1 + 2i é:
1 - iPara calcular a divisão de números complexos que ocorre em z, multiplicamos o numerador e o denominador de z pelo conjugado do denominador, isto é:
z = 1 + 2i . 1 + i
1 – i 1 + iz = (1 + 2i).(1 + i)
(1 – i).(1 + i)z = 1 + 2i + i + 2.i²
1 – i²z = 1 + 3i – 2
1 – (– 1)z = – 1 + 3i
2z = – 1 + 3 i
2 2Logo, a alternativa correta é a letra b.