Exercícios sobre função exponencial
Um paciente recebe uma injeção de material radioativo com meia-vida de 2 horas. Sabendo que foram aplicados 200 microgramas desse material, depois de 8 horas quanto ainda permanece no corpo do paciente?
A) 100 microgramas
B) 50 microgramas
C) 25 microgramas
D) 12,5 microgramas
E) 6,25 microgramas
Alternativa D
Pelo exposto no exercício temos a modelagem da função exponencial dada por:
\(f\left(x\right)=200\left(\frac{1}{2}\right)^x\), onde x são os períodos de 2 horas.
Como foi pedido o cálculo depois de 8 horas, teremos 4 períodos de 2 horas, levando assim a considerarmos o valor de x=4 .
\(f\left(4\right)=200\left(\frac{1}{2}\right)^4=\frac{200}{16}=12,5\ microgramas\)
Considere uma função exponencial da expressão \(f\left(x\right)={1000}^x\). Determine o valor de \(f\left(0,\bar{33}\right)\).
A) 10
B) 240
C) 333
D) 40
E) 33
Alternativa A
Pelo exposto no exercício temos a modelagem da função exponencial dada por:
\(f\left(x\right)={1000}^x\)
onde x assume valor dado por uma dízima periódica
\(0,333\ldots=\frac{3}{9}=\frac{1}{3}.\)
Substituindo esse valor, temos
\(f\left(\frac{1}{3}\right)={1000}^\frac{1}{3}=\sqrt[3]{1000}=10.\)
Sendo as funções \(g\left(x\right)=3^{x+27} \) e \(h\left(x\right)=9^{2x+3\ }\) dadas no conjunto dos números reais, determine o valor de x que as torna iguais nesse ponto.
A) 5
B) 7
C) 9
D) 11
E) 13
Alternativa B
O exercício nos pediu que as funções fossem iguais em um ponto, logo podemos escrever:
\(g(x)=h(x)\)
\(3^{x+27}=9^{2x+3}\)
\(3^{x+27}=\left(3^2\right)^{2x+3}\)
\(3^{x+27}=3^{4x+6}\)
Resolvendo, temos que:
\(4x+6=x+27\)
\(3x=21\)
\(x=7\)
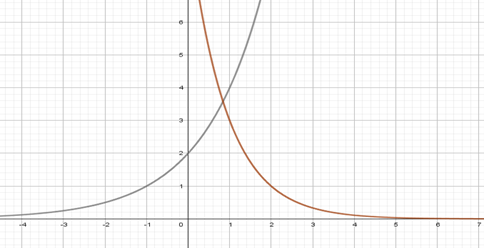
Na figura abaixo foi destacado o gráfico de duas funções exponenciais f(x) e g(x). Sabendo que f(x) é uma função crescente e g(x) decrescente, analise as alternativas abaixo sobre esse gráfico e marque a alternativa correta.
A) f(1)=3
B) f(2)=1
C) f(1)+g(2)=5
D) f(2)+g(1)=5
E) g(2)>3
Alternativa C
O exercício afirma que a f(x) é crescente, logo o gráfico dessa função é o de cor azul (ascendente), e pela mesma análise concluímos que g(x) é a função de cor vermelha (descendente). De posse desses resultados e com auxílio do gráfico, temos que \(f\left(2\right)>6, f\left(1\right)=4, \ g\left(1\right)=3 \ e\ g\left(2\right)=1\).
Analisando os itens, temos:
A) Falso, pois \(f(1)=4\).
B) Falso, pois \(f\ (2)>6\).
C) Verdadeiro, pois \(f\left(1\right)+g\left(2\right)=4+1=4\).
D) Falso, pelo próprio item C).
E) Falso, pois \(g(2)=1\).
Sendo \(f\left(x\right)=2^{x+1}\) definida no conjunto dos números reais, marque a alternativa que representa o esboço do gráfico dessa função.
A)
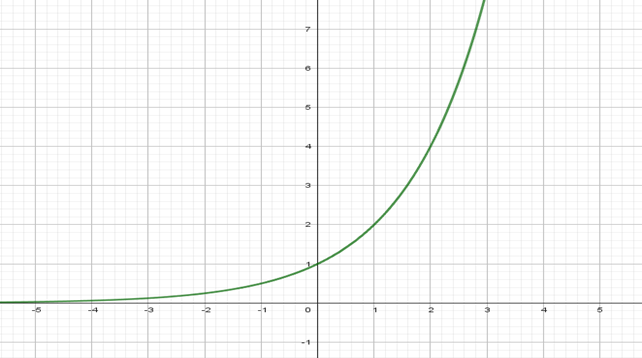
B)
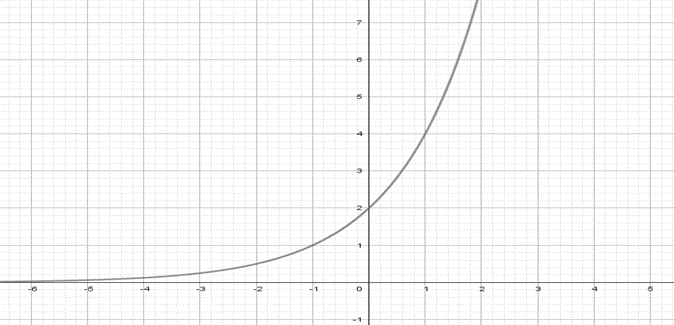
C)
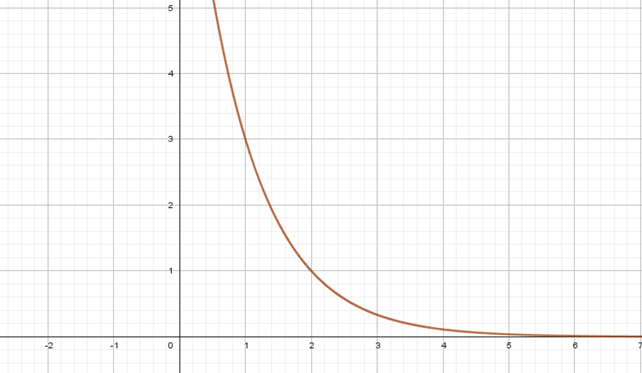
D)
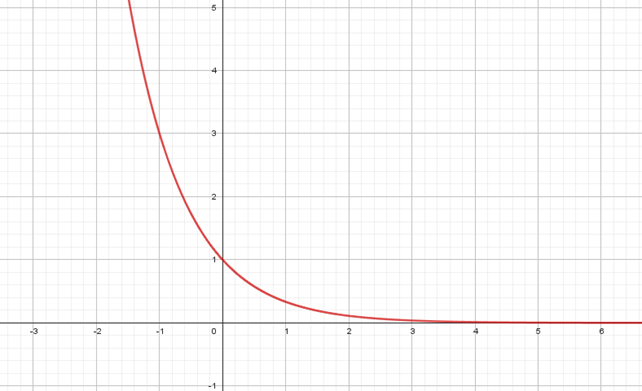
E)
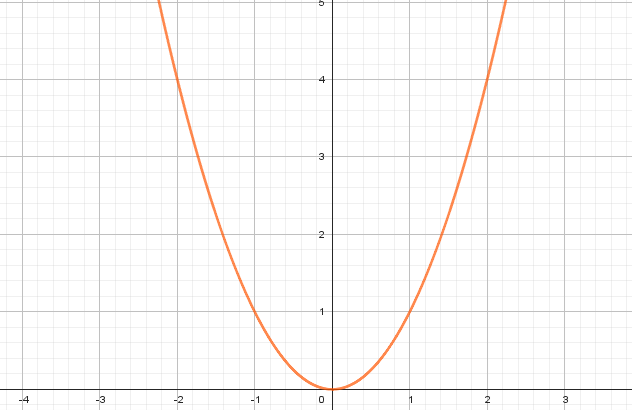
Alternativa B
Antes de analisar os itens, observamos que a função exponencial \(f\left(x\right)=2^{x+1}\) é crescente.
Com essa informação sabemos que os itens C) e D) são falsos por não serem gráficos de uma função crescente. O item E) é falso por ser gráfico de uma função do segundo grau (parábola).
Agora precisamos de alguns valores da função \(f\left(x\right)=2^{x+1}\).
O valor de \(f\left(0\right)=2^{0+1}=2^1=2\). Como o gráfico do item A) afirma que \(f\left(0\right)=1\), podemos desconsiderar esse item.
Com as conclusões acima, podemos afirmar que o único item possível é o B.
Sendo \(h\left(x\right)={0,5}^{x\ }\) definida no conjunto dos números reais, faça os cálculos e marque a alternativa correta da expressão \(h\left(-1\right)+h\left(-2\right)+h\left(1\right)+h(2)\) .
A) 0
B) 6,75
C) 4,25
D) 2,35
E) 1,75
Alternativa B
Primeiro determinaremos os valores de cada parte dessa expressão.
\(h\left(-1\right)={0,5}^{-1}=\left(\frac{1}{2}\right)^{-1}=2\)
\(h\left(-2\right)={0,5}^{-2}=\left(\frac{1}{2}\right)^{-2}=4\)
\(h\left(1\right)={0,5}^1=0,5\)
\(h\left(2\right)={0,5}^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}=0,25\)
Agora que estamos de posse dos resultados podemos efetuar a soma:
\(h\left(-1\right)+h\left(-2\right)+h\left(1\right)+h\left(2\right)=2+4+0,50+0,25=6,75\)
O número de casos de uma doença infecciosa dobra a cada 3 dias. Se houver 100 casos hoje, quantos casos haverá após 12 dias?
A) 400
B) 800
C) 1200
D) 1400
E) 1600
Alternativa E
Pelo exposto no exercício temos a modelagem da função exponencial dada por:
\(f\left(x\right)=100⸳2x\)
onde x são os períodos de 3 dias. Como foi pedido o cálculo depois de 12 dias, teremos 4 períodos de 3 dias, levando assim a considerarmos o valor de x=4.
\(f\left(4\right)=100\left(2\right)^4=1600\ casos\)
Um carro novo é comprado por R$ 40.000 e desvaloriza a uma taxa de 15% ao ano. Quanto valerá o carro após 3 anos? Marque a alternativa que possui uma função exponencial modelando a situação descrita.
A) \(40.000\left(0,15\right)^3\)
B) \(40.000\left(15\right)^3\)
C) \(40.000\left(0,85\right)^3\)
D) \(40.000\left(1,15\right)^3\)
E) \(40.000\left(0,55\right)^3\)
Alternativa C
Com base nos dados do exercício a modelagem da função é do tipo exponencial, dada por:
\(f\left(t\right)=V\left(1+i\right)^t\)
onde V é o valor de compra do carro, t é quantidade de períodos e i é a taxa.
Como é uma desvalorização, temos que \(i=-15%=-0,15\)
\(f\left(3\right)=40000\left(1-0,15\right)=40000(0,85)\)
Resolvendo o sistema \(\left\{{4^{x-y}=\sqrt2\atop2^{x+2y}=\sqrt[3]{2}}\right.\), temos que o valor de \(36y+18x \) é:
A) 2
B) 4
C) 6
D) 8
E) 54
Alternativa C
Primeiro vamos organizar o sistema de modo a ter a mesma base nos dois lados da igualdade.
\(\left\{{\left(2^2\right)^{x-y}=2^\frac{1}{2}\atop2^{x+2y}=2^\frac{1}{3}}\right.\)
\(\left\{{\left(2\right)^{2x-2y}=2^\frac{1}{2}\atop2^{x+2y}=2^\frac{1}{3}}\right.\)
Agora podemos reorganizar o sistema nas variáveis x e y, ficando com o seguinte sistema equivalente:
\(\begin{cases} 2x-2y=\frac{1}{2}\\ x+2\ y=\frac{1}{3} \end{cases}\)
Resolvendo esse sistema por método de soma, temos de forma direta \(3x=\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\). Logo temos que \(x=\frac{5}{18}\). Substituindo em \(x+2y=\frac{1}{3}\), temos \(2y=-\frac{5}{18}+\frac{1}{3}=\frac{1}{18}\), a partir de que concluímos que \(y=\frac{1}{36}\).
Podemos terminar o exercício efetuando a soma \(36y+18x=1+5=6\)
Suponha que uma colônia de bactérias esteja crescendo em um cubo de gelatina cuja aresta é 9 cm. A taxa de crescimento das bactérias é de 200% a cada hora. No início, a colônia ocupa um volume de 1 centímetro cúbico dentro do cubo. O volume da colônia de bactérias aumenta à medida que ela cresce. Quanto tempo levará para que essa colônia ocupe todo o volume desse cubo?
A) 3 horas
B) 6 horas
C) 9 horas
D) 12 horas
E) 15 horas
Alternativa B
A capacidade da gelatina é \(V=9^3=729{cm}^3\).
Sabendo que a taxa de crescimento é 200%=2, temos que a modelagem da função exponencial é dada por \(f\left(t\right)=1\cdot\left(1+2\right)^t=3^t\).
Igualando, temos que \(3^t=729=3^6\), logo t=6 horas.
Suponha que a população de uma colônia de 800 bactérias do tipo A que se triplica a cada 3 horas e uma segunda colônia de 2700 bactérias do tipo B que se duplica a cada 3 horas. Quanto tempo levará para que o número de bactérias dessas duas colônias seja o mesmo?
A) 6 horas
B) 4 horas
C) 9 horas
D) 8 horas
E) 3 horas
Alternativa C
De acordo com o enunciado do exercício temos que a modelagem do crescimento de bactérias é dado por uma função exponencial. Agora vamos modelar o crescimento de cada população.
- População de bactérias do tipo A: \(f\left(t\right)=800⸳3t\) (onde t representa o número de períodos de 3 horas).
- População de bactérias do tipo B:\(f\left(t\right)=2700⸳2t \) (onde t representa o número de períodos de 3 horas).
Igualando essas duas funções, temos:
\(800⸳3t=2700⸳2t\)
\(\frac{800}{2700}=\frac{2^t}{3^t}\)
\(\frac{8}{27}=\frac{2^t}{3^t}\)
\(\frac{2^3}{3^3}=\frac{2^t}{3^t}\)
\(\left(\frac{2}{3}\right)^3=\left(\frac{2}{3}\right)^t\)
Dessa igualdade concluímos que t=3. Como temos 3 períodos de 3 horas, podemos afirmar que após 9 horas as duas colônias terão a mesma quantidade de indivíduos.
Sendo uma função exponencial definida por \(f\left(x+1\right)=200\cdot\left(a+4\right)^x\), determine o valor de a para que a \(f\left(2\right)=400\).
A) 2
B) -1
C) 3
D) -2
E) -3
Alternativa D
O enunciado afirma que \(f\left(2\right)=400\). Pela modelagem da função \(f\left(x+1\right)=200\cdot\left(a+4\right)^x\), concluímos que \(x=1\). Igualando as duas expressões, temos:
\(200\cdot\left(a+4\right)^1=400\)
\(\left(a+4\right)=\frac{400}{200}\)
\(a+4=2\)
\(a=-2\)
