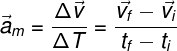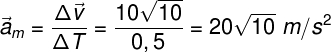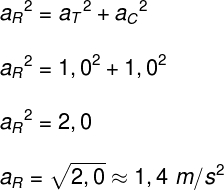Exercícios sobre aceleração vetorial média
Um carro move-se em linha reta a uma velocidade de 30 m/s. Ao avistar um obstáculo, o motorista faz uma curva brusca, alterando a direção da velocidade do carro para uma direção perpendicular, passando a se mover a 10 m/s. Admitindo que a curva foi realizada em um intervalo de tempo de 0,5 segundo, a aceleração vetorial média desse veículo foi de:
a) 3√10 m/s²
b) 30 m/s²
c) √10 m/s²
d) 10 m/s²
e) 20√10 m/s²
Letra E
Podemos calcular a aceleração vetorial média por meio da seguinte definição:
Como as duas velocidades fornecidas no exercício são perpendiculares entre si, é necessário aplicarmos o Teorema de Pitágoras (a² = b² + c²) sobre elas. Dessa forma, teremos que:
No cálculo acima, usamos o sinal positivo para calcularmos a variação da velocidade, pois as duas velocidades são perpendiculares entre si. Por fim, dividimos o resultado obtido pelo intervalo de tempo informado pelo enunciado:
Uma roda gigante tem aceleração tangencial de 1,0 m/s², e sua aceleração centrípeta tem o mesmo módulo. A aceleração vetorial média resultante nessa roda gigante é de:
a) 2,0 m/s²
b) 1,4 m/s²
c) 4,0 m/s²
d) 4,1 m/s²
e) 2,2 m/s²
Letra B
Como as acelerações tangencial e centrípeta são sempre perpendiculares entre si, usamos o Teorema de Pitágoras para calcularmos o módulo da aceleração vetorial resultante entre elas:
Sobre o conceito de aceleração vetorial média, assinale a alternativa que apresenta a informação correta:
a) Por ser uma aceleração média, ela fornece-nos o valor da aceleração no instante desejado.
b) Toda aceleração vetorial deve apresentar módulo, direção e sentido.
c) Trata-se de uma aceleração que apresenta somente módulo.
d) Não pode ser dividida em mais de uma componente.
Letra B
Vamos analisar as alternativas:
a) FALSA – Quem pode informar-nos a aceleração de instante em instante é a aceleração instantânea.
b) VERDADEIRA – Todas as grandezas vetoriais têm módulo, direção e sentido.
c) FALSA – Essa afirmação só é válida para acelerações escalares.
d) FALSA – Toda aceleração vetorial pode ser dividida em suas componentes, por se tratar de um vetor.
Um objeto cai em queda livre com aceleração constante e igual a 10 m/s². Um vento assopra o objeto em uma direção perpendicular, paralela ao solo, acelerando-o em 2 m/s². O módulo da aceleração vetorial resultante desse objeto é igual a:
a) 10√2 m/s²
b) 12 m/s²
c) 2√26 m/s²
d) 12√2 m/s²
e) 8 m/s²
Letra C
Para calcularmos o módulo da aceleração vetorial resultante, devemos aplicar o Teorema de Pitágoras às duas acelerações, que são perpendiculares. Em seguida, devemos fatorar o resultado:
