Exercícios sobre circuitos elétricos em série
Esta lista de exercícios trata da associação de resistores em série. Nesse tipo de associação, todos os resistores são atravessados pela mesma corrente elétrica.
Publicado por: Thiago Tavares da CostaQuestões
-
Questão 1
Um artista, para preparar a iluminação de um palco, decide conectar diversas lâmpadas iguais em uma associação em série. Após ligar a associação em uma fonte elétrica, o que ocorre caso uma das lâmpadas queime?
a) As outras lâmpadas permanecem acesas, porém com brilho maior.
b) As outras lâmpadas permanecem acesas, porém com o mesmo brilho.
c) As outras lâmpadas também apagam.
d) As outras lâmpadas permanecem acesas, porém brilham menos.
Letra C. Em uma ligação em série, a corrente elétrica é a mesma em todas as lâmpadas em funcionamento. Com isso, caso uma não funcione mais, isso fará que com a corrente elétrica não consiga mais percorrer o circuito, apagando todas as lâmpadas.
-
Questão 2
Um prestador de serviço, buscando um ponto de energia, conecta uma lâmpada ligada em série com seu ferro de solda. Comparando com o funcionamento de cada aparelho individualmente em condições normais, é correto afirmar que:
a) ambos funcionarão com seu brilho e potência normais.
b) a lâmpada ficará mais brilhante e o ferro de solda menos potente.
c) ambos funcionarão, porém com brilho e potência mais fracos.
d) o ferro de solda fará com que a lâmpada queime pela sobrecarga.
Letra C. Em uma ligação em série, a tensão é dividida entre os aparelhos em funcionamento. Por mais que a corrente elétrica seja a mesma, ela será consideravelmente menor do que a exigida naturalmente em condições normais.
-
Questão 3
Três resistores em série, de valores 10 Ω, 20 Ω e 30 Ω, respectivamente, são conectados em série e ligados a uma bateria ideal. Em qual dos resistores listados a tensão será maior?
a) 10Ω.
b) 20Ω.
c) 30Ω.
d) É a mesma em todos.
Letra C. De acordo com a Lei de Ohm (U = R · i), como a corrente elétrica é constante em todos os resistores, a tensão será maior justamente no resistor com a maior resistência.
-
Questão 4
Uma estudante, para incrementar um trabalho de ciências que consistia na construção de um circuito em série conectado a uma bateria ideal, decide instalar outra lâmpada idêntica às demais. O que ocorrerá com o circuito após ser ligado?
a) O brilho de cada lâmpada aumentará.
b) O brilho de cada lâmpada diminuirá.
c) O brilho de cada lâmpada permanecerá o mesmo.
d) As lâmpadas se apagarão.
Letra B. Com a adição de mais uma lâmpada, a resistência equivalente do circuito irá aumentar e, com isso, a corrente elétrica a ser percorrida irá diminuir. Como consequência, a potência das lâmpadas será menor e, com isso, o brilho também será menor.
-
Questão 5
Uma bateria de 12 V alimenta um circuito em série com dois resistores. Sabendo que, no primeiro resistor, a tensão obtida é de 8V, qual é a tensão no segundo?
a) 4V.
b) 8V.
c) 12V.
d) 20V.
Letra A. Em um circuito em série, a tensão em cada resistor é a soma da tensão total, logo:
12V = 8V + U2
U2 = 4V.
-
Questão 6
Por que lanternas antigas, que utilizavam diversas pilhas em série, paravam de funcionar de forma repentina?
a) Porque as pilhas se descarregam de forma desigual, mas todas continuam fornecendo energia.
b) Porque, mesmo que apenas uma pilha fique descarregada, isso já é suficiente para interromper o fornecimento de energia elétrica do sistema.
c) Porque a resistência interna de cada pilha aumenta de forma diferente.
d) Porque a tensão total cai gradualmente, mas a corrente se mantém constante.
Letra B. As pilhas, conectadas em série, formam um caminho único para a corrente do circuito. Caso uma pilha se esgote completamente, ela se transformará em uma chave aberta no circuito, interrompendo a corrente elétrica.
-
Questão 7
Ao utilizar um voltímetro para medir a diferença de potencial entre os terminais de uma lâmpada acesa em um circuito em série, o valor obtido será:
a) igual à tensão da fonte.
b) menor que a tensão da fonte.
c) maior que a tensão da fonte.
d) nulo.
Letra B. O voltímetro irá medir a tensão nos terminais da pilha, logo cada lâmpada acesa em um circuito em série representa uma pequena fração da tensão total da fonte elétrica. Por isso, a tensão medida em cada pilha será obrigatoriamente menor que a da fonte.
-
Questão 8
Qual a principal característica que define, conceitualmente adequado, se dois ou mais componentes elétricos estão conectados em série?
a) Eles possuem uma tensão elétrica igual à fonte.
b) A corrente elétrica de cada componente depende do valor da resistência elétrica.
c) A resistência equivalente irá diminuir conforme mais elementos forem adicionados.
d) Os elementos são percorridos pela mesma corrente elétrica.
Letra D. Em uma ligação em série, a corrente elétrica é a mesma em todas as lâmpadas em funcionamento.
-
Questão 9
(UERJ 2022) O circuito abaixo representa uma instalação elétrica, sendo a corrente registrada no amperímetro A igual a 100 mA.
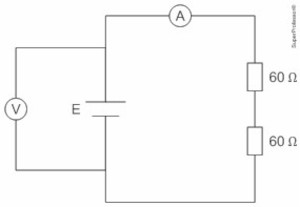
A tensão elétrica, em volts, indicada no voltímetro V, é igual a:
a) 8
b) 10
c) 12
d) 14
Alternativa C
Pela 1ª lei de Ohm, a indicação do voltímetro será de:
U = Req · i
U = (60 + 60) · 0,1
∴ U = 12 V -
Questão 10
(Eear 2018) Em uma aula de laboratório, o professor montou um circuito com 3 resistores ôhmicos R1, R2 e R3 associados a uma fonte de alimentação ideal (Vt) conforme o circuito abaixo. E solicitou ao aluno que, usando um amperímetro ideal, medisse o valor da intensidade de corrente elétrica que flui através de R2.
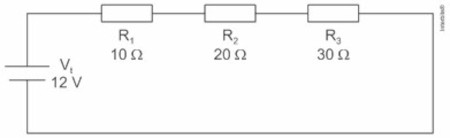
O aluno, porém fez a ligação do amperímetro (A) da maneira indicada na figura a seguir. Com base nisso, assinale a alternativa que representa o valor indicado, em ampères, no amperímetro.
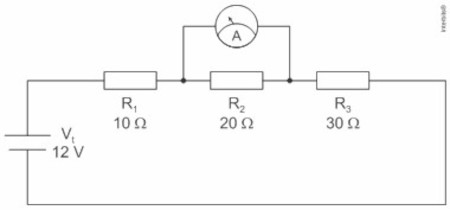
a) 0,0
b) 0,2
c) 0,3
d) 0,4
Letra C. Como o amperímetro ideal possui resistência nula, é como se R2 estivesse em curto nesse caso, portanto:
Req = R1 + R3 = 10 + 30 → Req = 40 Ω
Vt = Req · i → 12 = 40 · i
∴ i = 0,3 A -
Questão 11
(UFU 2016) Dispondo de algumas pilhas idênticas, de resistência interna desprezível, fios e pequenas lâmpadas de mesma potência, um estudante monta alguns tipos diferentes de circuitos elétricos, conforme a figura a seguir.
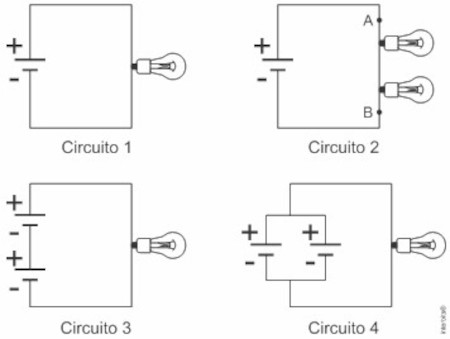
Em relação aos fios ideais, considere as afirmativas sobre a corrente que circula pelos circuitos.
I. A corrente circula pelo circuito 2 é menor que a do circuito 4.
II. A corrente que circula pelo circuito 1 é menor que a do circuito 3.
III. A corrente que circula pelo circuito 1 é menor que a do circuito 4.
IV. No circuito 2, quando a corrente passa pelo ponto A, ela é maior do que quando passa pelo B.
Assinale a alternativa que apresenta apenas afirmativas corretas.
a) I e II.
b) II e III.
c) I e IV.
d) III e IV.
Letra A
Quando um circuito está em série, as resistências são somadas (Req = R1 + R2 + … + Rn), quando a ddp. está em série, ela é somada (Ueq = U1 + U2 + … + Un), e quando a ddp está em paralelo, nada muda.
\(\begin{array}\\ i_1 = \dfrac{U}{R} \\ i_2 = \dfrac{U}{2R} \\ i_3 = \dfrac{2U}{R} \\ i_4 = \dfrac{U}{R} \end{array} \rangle i_3> i_1 = i_4>i_2\)
-
Questão 12
(Espcex (Aman) 2013) Quatro lâmpadas ôhmicas idênticas A, B, C e D foram associadas e, em seguida, a associação foi ligada a um gerador de energia elétrica ideal. Em um dado instante, a lâmpada A queima, interrompendo o circuito no trecho em que ela se encontra. As lâmpadas B, C e D permanecem acesas, porém o brilho da lâmpada B aumenta e o brilho das lâmpadas C e D diminui. Com base nesses dados, a alternativa que indica a associação formada por essas lâmpadas é:
a)
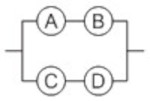
b)
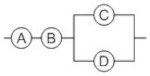
c)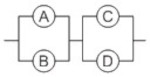
d)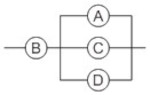
e)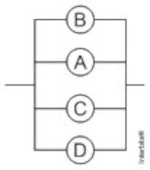
Letra C. Se A queima e as outras não se apagam, elas não podem estar em série, e, se o brilho delas se altera, elas não podem estar as quatro em paralelo. Como o brilho de B aumenta, a corrente em B aumenta; como o brilho de C e D diminui, a corrente nelas diminui, implicando que a resistência equivalente do circuito aumenta. Essas análises nos levam à alternativa [C].