Exercícios sobre aumento linear transversal

A posição, a altura de um objeto e sua respectiva imagem formada por uma lente esférica podem ser determinadas fazendo-se o uso da equação do aumento linear transversal. Publicado por: Domiciano Correa Marques da Silva

Imprimir

Questão 1

Imagine um objeto sobre o eixo principal de uma lente divergente de distância focal de 20 cm. Supondo que o objeto tenha tamanho de 8 cm e que ele esteja localizado a uma distância de 60 cm da lente, determine o tamanho da imagem formada e marque a alternativa correta.

a) + 1,25 cm
b) – 1,25 cm
c) 1,57 cm
d) – 1,98 cm
e) 1,98 cm

Ver resposta

Resposta

Primeiramente devemos retirar todas as informações fornecidas pelo exercício.

o = + 8 cm (altura); f = - 20 cm (divergente); p = + 60 cm; p’ = ?

A partir da equação do aumento linerar podemos escrever que:

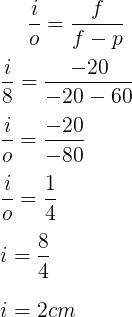
Alternativa D

Questão 2

Imagine uma lente convergente e um objeto que está localizado a 60 cm dessa lente. A distância focal dessa lente vale 20 cm. Determine o aumento linear e marque a opção correta.

a) 0,5
b) 1
c) -0,5
d) -1
e) 2

Ver resposta

Resposta

Primeiro é preciso saber qual é a distância da imagem à lente. Para isso, usaremos a Equação de Gauss. Como p = +60 cm (objeto sempre real) e f = +20 cm (convergente) calculemos, então, p’:

Alternativa C

Questão 3

(UNESP-96) Na figura, estão representados, esquematicamente, o perfil de uma lente esférica delgada, de vidro, imersa no ar, e a trajetória de um raio de luz que parte de um ponto O do eixo principal, atravessa a lente e passa novamente pelo eixo principal no ponto I.

Admitindo-se válidas as condições de estigmatismo de Gauss, calcule a distância focal dessa lente e marque a alternativa certa.

a) 6 cm
b) 8 cm
c) 9 cm
d) 4 cm
e) 5 cm

Ver resposta

Resposta

Retirando todos os dados fornecidos pelo exercício, temos:

p = 15 cm; p’ = 10 cm; f = ?

Fazendo uso da Equação de Gauss, podemos determinar o valor da distância focal:

Alternativa A

Questão 4

(UEM) Um objeto de tamanho igual a 15 cm está situado a uma distância igual a 30 cm de uma lente. Verifica-se que a lente forma uma imagem virtual do objeto cujo tamanho é igual a 3 cm. Qual é o módulo da distância (em cm) da imagem à lente?

a) 4 cm
b) 5 cm
c) 6 cm
d) 7 cm
e) 8 cm

Ver resposta

Resposta

Primeiro retiramos todos os dados do exercício e depois realizamos os cálculos:

o = 15 cm; i = + 3 cm; p = 30 cm; p’ = ?