Exercícios sobre campo elétrico

Analise as alternativas abaixo referentes às unidades de medida estudadas em eletrostática:

I. A unidade de medida da carga elétrica é metros por segundo.

II. A unidade de medida do campo elétrico é Newton por Coulomb.

III. A unidade de medida da força elétrica é Newton.

IV. A unidade de medida da constante eletrostática do meio é representada por \({\left(N\cdot m\right)^2/C}^2\) .

Qual alternativa está correta?

A) II, III e IV.

B) I, III e IV.

C) I, II e III

D) Todas estão corretas.

E) Todas estão incorretas.

Qual o valor da intensidade do campo elétrico no vácuo, a 13 cm  de uma carga elétrica de 2,6 n C?

A) \(1,3846\cdot{10}^9\ N/C\)

B) \(1,3846\cdot{10}^3\ N/C\)

C) \(1,3846\cdot{10}^{10}\ N/C\)

D) \({1,3846\cdot10}^{11}\ N/C\)

E) \(1,3846\cdot{10}^2\ N/C\)

Uma carga elétrica pontual de valor -24 μC  é posta em determinado lugar no vácuo, estando sujeita a uma força elétrica de valor 360 N . Considerando isso, encontre o módulo do campo elétrico dessa carga nesse lugar.

A) \(1,5\cdot{10}^5\ N/C\)

B) \(1,5\cdot{10}^6\ N/C\)

C) \(1,5\cdot{10}^7\ N/C\)

D) \(1,5\cdot{10}^8\ N/C\)

E) \(1,5\cdot{10}^9\ N/C\)

Duas cargas elétricas são separadas a uma distância de 300 cm  no vácuo. Encontre o valor da força elétrica entre elas e o campo elétrico da carga de menor valor, sabendo que suas cargas são 3,2 C  e 5,6 C .

\(A) 5,6\cdot{10}^9\ N; 5,6\cdot{10}^{9\ }N/C.\)

\(B) 5,6\cdot{10}^9\ N; 17,92\cdot{10}^{9\ }N/C.\)

\(C) 17,92\cdot{10}^9\ N; 17,92\cdot{10}^{9\ }N/C.\)

\(D) 0\ N; 0\ N/C.\)

\(E)\ 17,92\cdot{10}^9\ N; 5,6\cdot{10}^{9\ }N/C.\)

Determine a intensidade do campo elétrico no vácuo de uma carga elétrica de 12 mC  a 2,5  metros.

A) \(1,728\cdot{10}^7\ N/C\)

B) \(1,425\cdot{10}^{-6}\ N/C\)

C) \(1,923\cdot{10}^{-3}\ N/C\)

D) \(1,631\cdot{10}^{10}\ N/C\ \)

E) \(1,3728\cdot{10}^8\ N/C\)

Uma carga elétrica de valor A produz um campo elétrico de 2500 N/C  e possui uma força elétrica atrativa de 100 N  com outra carga de valor B, que é o dobro de A. Considerando isso, determine o valor da carga Q e da carga q.

A) 0,03 C  e 0,06 C

B) 0,05 C  e 0,1 C

C) 0,04 C  e 0,08 C

D) 0,01 C  e 0,02 C

E) 0,02 C  e 0,04 C

A uma distância de 50 metros, temos o campo elétrico produzido por uma carga Q, cujo valor é de 12 C. Sabendo que a constante eletrostática do vácuo vale 9 ∙10⁹  N ∙ m² / C² , encontre o valor desse campo elétrico.

A) \(4,32\cdot{10}^9\ N/C\)

B) \(2,16\cdot{10}^{11\ }N/C\)

C) \(0\ N/C\)

D) \(2,16\cdot{10}^9\ N/C\)

E) \(4,32\cdot{10}^7\ N/C\)

De acordo com seus estudos a respeito do campo elétrico, alguma(s) das fórmulas abaixo não serve(m) para calculá-lo.

I. \(E=k\cdot\frac{Q}{d^2}\)

II. \(E=q\cdot V\)

III. \(E=\frac{F}{q}\)

Qual alternativa está correta?

A) I e II.

B) I e III.

C) II e III.

D) Todas estão corretas.

E) Todas estão incorretas.

(Uece) Considere o campo elétrico gerado por duas cargas elétricas puntiformes, de valores iguais e sinais contrários, separadas por uma distância d. Sobre esse vetor campo elétrico nos pontos equidistantes das cargas, é correto afirmar que

A) tem a direção perpendicular à linha que une as duas cargas e o mesmo sentido em todos esses pontos.

B) tem a mesma direção da linha que une as duas cargas, mas varia de sentido para cada ponto analisado.

C) tem a direção perpendicular à linha que une as duas cargas, mas varia de sentido para cada ponto analisado.

D) tem a mesma direção da linha que une as duas cargas e o mesmo sentido em todos esses pontos.

(Unesp) Modelos elétricos são frequentemente utilizados para explicar a transmissão de informações em diversos sistemas do corpo humano. O sistema nervoso, por exemplo, é composto por neurônios (figura 1), células delimitadas por uma fina membrana lipoproteica que separa o meio intracelular do meio extracelular. A parte interna da membrana é negativamente carregada e a parte externa possui carga positiva (figura 2), de maneira análoga ao que ocorre nas placas de um capacitor.

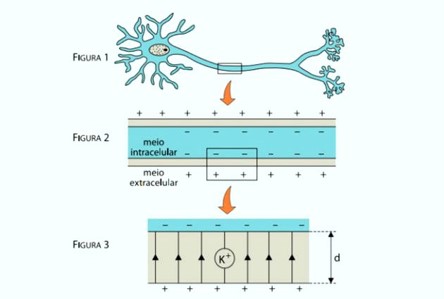
A figura 3 representa um fragmento ampliado dessa membrana, de espessura d, que está sob ação de um campo elétrico uniforme, representado na figura por suas linhas de força paralelas entre si e orientadas para cima. A diferença de potencial entre o meio intracelular e o extracelular é V. Considerando a carga elétrica elementar como e, o íon de potássio K+, indicado na figura 3, sob ação desse campo elétrico, ficaria sujeito a uma força elétrica cujo módulo pode ser escrito por:

A) \(e\cdot V\cdot d\)

B) \(\frac{e\ \cdot\ d}{V}\)

C) \(\frac{V\ \cdot\ d}{e}\)

D) \(\frac{e}{V\ \cdot\ d}\)

E) \(\frac{e\ \cdot\ V}{d}\)

(Uece) Precipitador eletrostático é um equipamento que pode ser utilizado para remoção de pequenas partículas presentes nos gases de exaustão em chaminés industriais. O princípio básico de funcionamento do equipamento é a ionização dessas partículas, seguida de remoção pelo uso de um campo elétrico na região de passagem delas. Suponha que uma delas tenha massa m, adquira uma carga de valor q e fique submetida a um campo elétrico de módulo E. A força elétrica sobre essa partícula é dada por:

A) \(m\cdot q\cdot E\)

B) \(m\cdot E/q\cdot b\)

C) \(q/E\)

D) \(q\cdot E\)

(FEI SP) A intensidade do vetor campo elétrico num ponto P é 6∙10⁵ N/C . Uma carga puntiforme q=3∙10^-6 C colocada em P ficará sujeita a uma força elétrica cuja intensidade:

A) para o cálculo, necessita da constante do meio em que a carga se encontra.

B) para o cálculo, necessidade da distância.

C) vale 2 N .

D) vale 2∙10^-11 N .

E) vale 1,8 N .