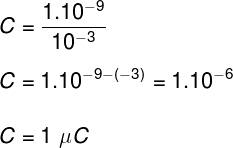Exercícios sobre capacitores
(UFV-2005) Duplicando-se a diferença de potencial entre as placas de um capacitor, é CORRETO afirmar que:
a) a carga e a capacitância do capacitor também são duplicadas
b) a carga e a capacitância do capacitor permanecem constantes
c) a carga do capacitor é duplicada, mas sua capacitância permanece constante
d) a carga e a capacitância do capacitor são reduzidas à metade dos valores iniciais
e) a carga do capacitor é duplicada, e sua capacitância é dividida pela metade
Letra C
Podemos calcular a capacitância de um capacitor por meio da seguinte equação:
Analisando a equação acima, pode-se notar que a capacitância depende de fatores geométricos, tais como a área das placas do capacitor e a distância entre as placas, além da permissividade dielétrica do meio inserido entre elas. Portanto, a capacitância permanece constante.
Duplicando-se a diferença de potencial entre as placas do capacitor, a sua carga tende a dobrar, de acordo com a seguinte equação:
Multiplicando cruzado os termos da equação acima, temos a seguinte relação para a carga elétrica:
Para uma tensão 2V, teremos o seguinte cálculo:
Portanto, a carga elétrica dobra de módulo, enquanto a capacitância permanece constante.
Um capacitor consegue armazenar cargas de até 1 nC para uma diferença de potencial entre suas placas de 1 mV. Indique, entre as alternativas abaixo, o módulo da capacitância desse dispositivo:
a) 3.10-3 F
b) 1.10-6 F
c) 1.10-3 F
d) 5.10-6 F
e) 4.10-5 F
Letra B
Podemos relacionar a capacitância à quantidade de carga (Q) armazenada em um capacitor para uma dada diferença de potencial (V) pela equação abaixo:
.jpg){kind=small}
De acordo com os dados fornecidos no enunciado do exercício, temos que:
Lembre-se: 1 nC = 1 nanoCoulomb (10-9 C) e 1 mV = 1 miliVolt (10-3 V). Portanto, a alternativa correta é a letra B.
Veja também: Prefixos do Sistema Internacional de Unidades
Entre as placas dos capacitores, costuma-se inserir um material dielétrico preferencialmente ao vácuo. A inserção de um material dessa natureza entre as placas de um capacitor:
a) aumenta a sua capacitância por causa da sua maior permissividade elétrica
b) aumenta a sua capacitância, diminuindo a quantidade de cargas entre as suas placas
c) não afeta a sua capacitância
d) diminui a sua capacitância, por causa da sua maior permissividade elétrica
e) não afeta a formação do campo elétrico entre as placas do capacitor
Letra A
Vamos analisar as alternativas:
a) VERDADEIRO – A constante de permissividade elétrica do vácuo é baixa – por isso, ao inserirmos um material dielétrico entre as placas do capacitor, aumenta-se a sua capacitância, já que é possível armazenar uma quantidade maior de cargas nesses materiais, para uma mesma diferença de potencial;
b) FALSO – O módulo da carga elétrica entre as placas pode aumentar, não diminuir;
c) FALSO – A capacitância aumenta ao inserirmos um meio dielétrico entre as placas do capacitor;
d) FALSO – A capacitância é afetada de modo que o seu valor aumente, uma vez que a inserção de um meio dielétrico entre suas placas aumenta a sua permissividade elétrica, em vez de diminui-la;
e) FALSO – A capacitância é afetada pela alteração da permissividade elétrica do meio, que é responsável por afetar a maneira como os campos elétricos se propagam em seu interior.
Em relação à capacitância de um capacitor de placas paralelas, assinale o que for FALSO:
a) a capacitância é diretamente proporcional à área dos capacitores
b) a capacitância é inversamente proporcional à distância entre os capacitores
c) a permissividade elétrica é uma característica que depende do material inserido entre as placas do capacitor
d) quanto maior for a capacitância de um capacitor, menos carga ele pode armazenar para uma determinada tensão elétrica
e) quanto menor for a capacitância de um capacitor, menos carga ele pode armazenar para uma determinada tensão elétrica
Letra C
A capacitância dos capacitores de placas paralelas é dada pela equação abaixo:
.jpg){kind=small}
Da relação acima, nota-se que a capacitância (C) é diretamente proporcional à área e à permissividade elétrica do meio inserido entre suas placas e inversamente proporcional à distância entre as placas (d).
No entanto, quanto maior for a capacitância do dispositivo, mais carga ele conseguirá armazenar para uma mesma tensão elétrica. Portanto, a alternativa falsa é a letra c.
