Exercícios sobre convergência de uma lente esférica
Esta lista de exercícios trata sobre a convergência de lentes esféricas. A capacidade das lentes de desviar a luz é medida por sua convergência.
Publicado por: Rafael HelerbrockQuestões
-
Questão 1
Algumas lentes esféricas e delgadas, quando imersas no ar, são capazes de separar os raios de luz, produzindo imagens exclusivamente virtuais. Essas lentes são chamadas de:
a) convergentes.
b) divergentes.
c) cilíndricas.
d) esféricas.
e) delgadas.
Letra B
As lentes capazes de separar os raios de luz, em vez de concentrá-los, são chamadas de lentes divergentes. As imagens produzidas pelas lentes divergentes são ditas virtuais, pois são formadas pelo cruzamento de prolongamentos de luz.
-
Questão 2
A propriedade de uma lente capaz de alterar a direção de propagação da luz que incide sobre ela é chamada de:
a) ampliação.
b) difração.
c) convergência.
d) reflexão.
e) interferência.
Letra C
A vergência (também chamada de convergência) mede o “grau” de uma lente, ou seja, a capacidade da lente de mudar a direção da luz que passa através dela.
-
Questão 3
Determinada lente esférica e delgada possui distância focal de 20 cm. Determine a dioptria dessa lente.
a) 0,05 di
b) 20 di
c) 5 di
d) 0,2 di
e) 3 di
Letra C
Podemos calcular a convergência de uma lente por meio da seguinte fórmula:
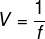
Na fórmula acima, f é a distância focal da lente, dada em metros (f = 0,2 m). Dessa forma:
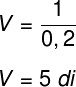
-
Questão 4
Uma lente com vergência igual a -2 di é uma lente:
a) convergente, de distância focal igual a 2 m.
b) delgada, de distância focal igual a -2 m.
c) convergente, de distância focal igual a -0,5 m.
d) divergente, de distância focal igual a -0,5 m.
e) esférica, de distância focal igual a -2 m.
Letra D
Quando o sinal da vergência de uma lente é negativo, entende-se que a lente em questão é divergente. Além disso, para que sua vergência seja igual a -2, seu foco deve ser igual a:
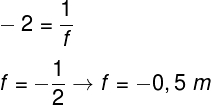
Portanto, a alternativa correta é a de letra D.
