Exercícios sobre o Dilatação linear dos sólidos
O gráfico abaixo representa a variação do comprimento de uma barra homogênea com a temperatura. Determine o coeficiente de dilatação linear de que a barra é constituída.
.gif)
.gif)
A figura a seguir mostra uma esfera de aço de 50,1 mm de diâmetro apoiada num anel de alumínio, cujo diâmetro interno é de 50,0 mm, ambos à mesma temperatura. Qual o acréscimo de temperatura que esse conjunto deve sofrer para que a esfera passe pelo anel?
(Dados: α aço = 1,08. 10-5 °C-1 e α al = 2,38 . 10-5 °C-1)
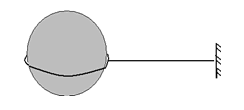
Devemos admitir que quando a esfera passa pelo anel, o diâmetro da esfera de aço (L aço ) é igual ao diâmetro interno do anel de alumínio (L al ). Portanto, basta determinar o valor de ∆T para que essa igualdade ocorra.
Assim, da expressão L = Lo + ∆L, podemos fazer:
L aço = L al → Lo aço + ∆L aço = Lo al + ∆L al → ∆L al - ∆L aço = Lo aço - Lo al (1)
Substituindo a expressão ∆L = α Lo ∆T em 1, obtemos:
α al Lo al ∆T - α aço Lo aço ∆T = Lo aço - Lo al
2,38.10-5.50,0.∆T - 1,08.10-5.50,1.∆T = 50,1 – 50,0
119.10-5 ∆T – 54,1. 10-5∆T = 0,1
64,9.10-5 ∆T = 0,1
∆T = 154 °C
Duas barras homogêneas, A e B, tem seu comprimento L em função da temperatura variando de acordo com o gráfico.
Determine os coeficientes de dilatação linear α A e α B dos materiais que constituem as barras.
.gif)
.gif)
A extensão de trilhos de ferro sofre dilatação linear, calcule o aumento de comprimento que 1000 m dessa ferrovia sofre ao passar de 0 °C para 20 °C, sabendo que o coeficiente de dilatação linear do ferro é 12.10-6 °C-1.
Obs: Aumento de comprimento sempre indica variação, ou seja, ∆L.
∆L = Lo α ∆T (o primeiro passo é substituir os valores dados na equação)
∆L = 1000. 12.10-6 .20
∆L = 20 000. 12.10-6 (nesse momento foi multiplicado os termos inteiros para depois trabalharmos com o expoente de base 10).
∆L = 24.10-2 (transformação de notação científica para forma decimal).
∆L = 0,24 m
