Exercícios sobre dilatação térmica
(Fuvest) Para ilustrar a dilatação dos corpos, um grupo de estudantes apresenta, em uma feira de ciências, o instrumento esquematizado na figura abaixo. Nessa montagem, uma barra de alumínio com 30 cm de comprimento está apoiada sobre dois suportes, tendo uma extremidade presa ao ponto inferior do ponteiro indicador e a outra encostada num anteparo fixo. O ponteiro pode girar livremente em torno do ponto O, sendo que o comprimento de sua parte superior é 10 cm e, o da inferior, 2 cm. Se a barra de alumínio, inicialmente à temperatura de 25ºC, for aquecida a 225ºC, o deslocamento da extremidade superior do ponteiro será, aproximadamente, de
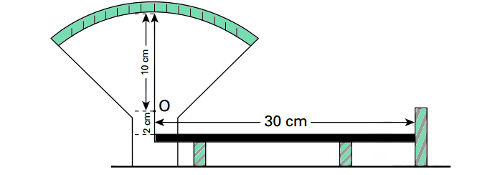
DADOS: O coeficiente de dilatação linear da barra é de 2x10 – 5 °C - 1
a) 1 mm
b) 3 mm
c) 6 mm
d) 12 mm
e) 30 mm
LETRA “C”
O deslocamento do ponteiro inferior será igual à dilatação sofrida pela barra, portanto:
Δlinf = l0 .α . ΔT
Δlinf = 30x10 – 2 . 2x10 – 5 . ( 225 – 25)
Δlinf = 60x10 – 7 . 200
Δlinf = 120x10 – 5
Δlinf = 1,2x10 – 3 = 1,2 mm
A figura abaixo mostra o deslocamento dos ponteiros. Como o deslocamento angular α é pequeno, podemos considerar que os deslocamentos das partes superior e inferior são praticamente retilíneos.
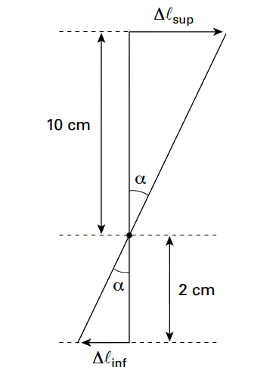
Aplicando a semelhança de triângulos, temos:
Δlsup = 10 portanto, Δlsup = 5 . Δlinf → Δlinf = 5 . 1,2mm = 6 mm
Δlinf 2
(UPE) Uma barra de coeficiente de dilatação α = 5π x 10-4ºC-1, comprimento 2,0 m e temperatura inicial de 25 ºC está presa a uma parede por meio de um suporte de fixação S. A outra extremidade da barra B está posicionada no topo de um disco de raio R = 30 cm. Quando aumentamos lentamente a temperatura da barra até um valor final T, verificamos que o disco sofre um deslocamento angular Δθ = 30º no processo. Observe a figura a seguir:
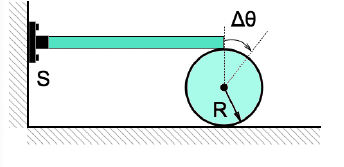
Supondo que o disco rola sem deslizar e desprezando os efeitos da temperatura sobre o suporte S e também sobre o disco, calcule o valor de T.
a) 50 °C
b) 75 °C
c) 125 °C
d) 300 °C
e) 325 °C
LETRA “B”
O deslocamento linear X correspondente ao giro de 30° do disco pode ser determinado pelo produto entre o ângulo em radianos e o raio do disco. Sabendo que 30° = π , temos:
6
X = ∆θ . R = π . 30 = 5 π cm
6
Sabendo que o deslocamento linear X corresponde à dilatação da barra, temos:
X = l0 .α . ΔT
5 π = 200 . 5π x 10-4 . ΔT
1 = 200 x 10-4 ΔT
ΔT . 2 x 10 – 2 = 1
ΔT = 1 = 50 °C
2 x 10 – 2
Como ΔT = T – T0 , temos:
50 = T – 25
T = 50 + 25
T = 75 °C
Uma barra de cobre com coeficiente de dilatação linear de 17x10 – 6 °C - 1 está inicialmente a 30 °C e é aquecida até que a sua dilatação corresponda a 0,17% de seu tamanho inicial. Determine a temperatura final dessa barra.
a) 85 °C
b) 65 °C
c) 105 °C
d) 130 °C
e) 80 °C
LETRA “D”
O aumento da barra deve corresponder a 0,17% do valor de seu comprimento inicial, portanto:
Δl = 0,17% l0
Δl = 0,0017 . l0
Δl = 1,7 x 10 – 3 . l0
Substituindo esse valor na equação da dilatação linear, temos:
Δl = l0 .α . ΔT
1,7 x 10 – 3 . l0 = l0 .α . ΔT
1,7 x 10 – 3 = α . ΔT
1,7 x 10 – 3 = ΔT. 17x10 – 6
ΔT = 1,7 x 10 – 3
17x10 – 6
ΔT = 100 °C
Como ΔT = T – T0 , temos:
100 = T – 30
T = 100 + 30
T = 130 °C
Uma lâmina bimetálica composta por zinco e aço está fixada em uma parede de forma que a barra de aço permanece virada para cima. O que ocorre quando a lâmina é resfriada?
Dado: αZINCO = 25x10 – 6 °C – 1 , αAÇO = 11x10 – 6 °C – 1
a) As duas barras sofrem a mesma dilatação.
b) A lâmina bimetálica curva-se para cima.
c) A lâmina bimetálica curva-se para baixo.
d) A lâmina quebra-se, uma vez que é feita de materiais diferentes.
e) Lâminas bimetálicas não podem ser resfriadas.
LETRA “C”
Como o zinco possui maior coeficiente de dilatação, ele sofrerá maior contração no resfriamento, puxando a barra de aço. Logo, o sistema curva-se para baixo.
