Exercícios sobre eletrodinâmica
(Enem) Alguns peixes, como o poraquê, a enguia-elétrica da Amazônia, podem produzir uma corrente elétrica quando se encontram em perigo. Um poraquê de 1 metro de comprimento, em perigo, produz uma corrente em torno de 2 ampères e uma voltagem de 600 volts.
O quadro apresenta a potência aproximada de equipamentos elétricos.
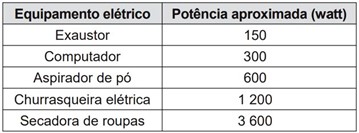
O equipamento elétrico que tem potência similar àquela produzida por esse peixe em perigo é o
A) exaustor.
B) computador.
C) aspirador de pó.
D) churrasqueira elétrica.
E) secadora de roupas.
Alternativa D.
Primeiramente, calcularemos a potência elétrica produzida pelo peixe, através da fórmula que a relaciona à corrente elétrica e à tensão elétrica:
\(P=U\cdot i\)
\(P=600\cdot2\)
\(P=1200\ W\)
De acordo com a tabela, o equipamento elétrico que tem a potência elétrica mais próxima da potência elétrica do peixe é a churrasqueira elétrica.
(UEL) Pela secção reta de um condutor de eletricidade passam 12,0 C a cada minuto. Nesse condutor, a intensidade da corrente elétrica, em ampères, é igual a:
A) 0,08
B) 0,20
C) 5,00
D) 7,20
E) 120
Alternativa B.
Primeiramente, convertemos o tempo de minutos para segundos:
\(1min{=60\ s}\)
Por fim, calculamos a corrente elétrica através da fórmula que a relaciona à carga elétrica e ao tempo:
\(i=\frac{Q}{t}\)
\(i=\frac{12}{60}\)
\(i=0,2\ A\)
(UEL) Pelo circuito elétrico esquematizado flui uma corrente elétrica:
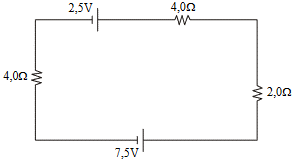
A diferença de potencial, em volts, nos terminais do resistor de 2,0 Ω e a potência nele dissipada, em watts, são, respectivamente,
A) 1,0 e 0,50
B) 1,0 e 2,0
C) 2,0 e 2,0
D) 2,0 e 4,0
E) 4,0 e 8,0
Alternativa A.
Para escrevermos a expressão algébrica adotaremos o sentido da corrente elétrica e da malha como no sentido horário. Então, iniciando do resistor de 4 Ω, obtemos:
\(+4i-7,5+2i+4i+2,5=0\)
\(+10i-5=0\)
\(10i=5\)
\(i=\frac{5}{10}\)
\(i=0,5\ A\)
A diferença de potencial elétrico no resitor é de 2,0 Ω, então calcularemos a partir da 1ª lei de Ohm:
\(U=R\cdot i\)
\(U=2\cdot0,5\)
\(U=1\ V\)
Já a potência elétrica dissipada nesse resistor será calculada através da sua fórmula:
\(P=R\cdot i^2\)
\(P=2\cdot{0,5}^2\)
\(P=0,5\ W\)
(Mackenzie) A diferença de potencial nos terminais de um receptor varia com a corrente conforme o gráfico abaixo.
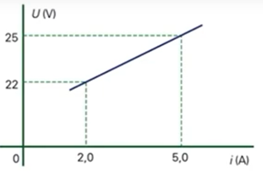
A força contraeletromotriz e a resistência interna desse receptor são, respectivamente:
A) 25 V e 50 Ω
B) 22 V e 2 Ω
C) 20 V e 1 Ω
D) 12,5 V e 2,5 Ω
E) 11 V e 1 Ω
Alternativa C.
Calcularmos a força contraeletromotriz e a resistência elétrica interna desse receptor elétrico através de um sistema de equações, utilizando para isso a equação dos receptores elétricos:
\(\begin{cases} 22=ε'+r'∙2\\ 25=ε'+r'∙5 \end{cases}\)
Primeiramente, isolaremos a resistência elétrica interna na primeira equação:
\(r^\prime=\frac{22-\varepsilon\prime}{2}\)
Depois, substituiremos essa expressão na segunda equação:
\(25=\varepsilon\prime+\left(\frac{22-\varepsilon\prime}{2}\right)\cdot5\)
\(25=\varepsilon\prime+\frac{110-5\varepsilon\prime}{2}\)
Multiplicando tudo por dois, encontraremos a força contraeletromotriz:
\(50=2\varepsilon\prime+110-5\varepsilon\prime\)
\(50-110=2\varepsilon\prime-5\varepsilon\prime\)
\(-60=-3\varepsilon\prime\)
\(60=3\varepsilon\prime\)
\(\varepsilon^\prime=\frac{60}{3}\)
\(\varepsilon^\prime=20\ V\)
Por fim, substituindo na equação em que isolamos, encontraremos a resistência elétrica interna:
\(^\prime=\frac{22-\varepsilon\prime}{2}\)
\(r^\prime=\frac{22-20}{2}\)
\(r^\prime=\frac{2}{2}\)
\(r^\prime=1\ \Omega\)
Um fio de cobre de resistividade elétrica de \(1,7\cdot{10}^{-6}\ \mathrm{\Omega}\cdot m\) tem 10 metros de comprimento e 0,1 m2 de área de secção transversal. A partir dessas informações, dê a sua resistência elétrica.
A) 1,7 Ω
B) 1,7∙10-1 Ω
C) 1,7∙10-2 Ω
D) 1,7∙10-3 Ω
E) 1,7∙10-4 Ω
Alternativa E.
Calcularemos a resistência elétrica do fio, através da 2ª lei de Ohm:
\(R=\rho\cdot\frac{L}{A}\)
\(R=1,7\cdot{10}^{-6}\cdot\frac{10}{0,1}\)
\(R=1,7\cdot{10}^{-6}\cdot100\)
\(R=1,7\cdot{10}^{-6}\cdot1\cdot{10}^2\)
\(R=1,7\cdot{10}^{-6+2}\)
\(R=1,7\cdot{10}^{-4\ }\Omega\ \)
Determine a capacitância equivalente de três capacitores de capacitância 2 mF, sabendo que dois eles estão associados em paralelo e um deles está associado em série.
Dica: Calcule primeiro a capacitância equivalente na associação em paralelo e depois na associação em série.
A) 1,16 mF
B) 1,25 mF
C) 1,34 mF
D) 2,42 mF
E) 2,67 mF
Alternativa C.
Primeiramente, calcularemos a capacitância equivalente dessa associação em paralelo, através da sua fórmula:
\({C_{12}=C}_1+C_2\)
\(C_{12}=2+\ 2\)
\(C_{12}=4\ mF\)
Por fim, calcularemos a capacitância equivalente na associação em série, através da sua fórmula:
\(C_{eq}=\frac{C_3\cdot C_{12}}{C_3+C_{12}}\)
\(C_{eq}=\frac{2\cdot4}{2+4}\)
\(C_{eq}=\frac{8}{6}\)
\(C_{eq}\cong1,34\ mF\)
Calcule a força eletromotriz (f.e.m.) de um gerador elétrico que tem uma resistência elétrica interna de 3 Ω, é percorrido por uma corrente elétrica de 7 A e conectado a uma ddp de 19 V .
A) 8 V
B) 19 V
C) 25 V
D) 32 V
E) 40 V
Alternativa E.
Calcularemos a força eletromotriz desse gerador elétrico, através da equação do gerador elétrico:
\(U=\varepsilon-r\cdot i\)
\(19=\varepsilon-3\cdot7\)
\(19=\varepsilon-21\)
\(\varepsilon=19+21\)
\(\varepsilon=40\ V\)
Calcule a resistência elétrica equivalente entre três resistores de 20 Ω cada, associados em série.
A) 20 Ω
B) 30 Ω
C) 40 Ω
D) 50 Ω
E) 60 Ω
Alternativa E.
Calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3\)
\(R_{eq}=20+20+20\)
\(R_{eq}=60\ \Omega\)
Um aparelho com uma resistência elétrica de 22 Ω é conectado a determinada diferença de potencial elétrico e passa a ser atravessado por uma corrente elétrica de 5 A. A partir dessas informações, determine a ddp em que se conecta o aparelho.
A) 50 V
B) 110 V
C) 180 V
D) 220 V
E) 300 V
Alternativa B.
Calcularemos a tensão elétrica através da sua fórmula:
\(U=R\cdot i\)
\(U=22\cdot5\)
\(U=110\ V\)
Calcule a resistência elétrica equivalente aproximada entre três resistores de 15 Ω , 20 Ω e 25 Ω , associados em paralelo.
A) 6,4 Ω
B) 7,5 Ω
C) 8,6 Ω
D) 9,7 Ω
E) 10,8 Ω
Alternativa A.
Calcularemos a resistência elétrica equivalente dos resistores associados em paralelo através da sua fórmula geral:
\(\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)
\(\frac{1}{R_{eq}}=\frac{1}{15}+\frac{1}{20}+\frac{1}{25}\)
\(\frac{1}{R_{eq}}=\frac{20+15+12}{300}\)
\(\frac{1}{R_{eq}}=\frac{47}{300}\)
\(R_{eq}=\frac{300}{47}\)
\(R_{eq}\approx6,4\ \Omega\)
O circuito elétrico de um liquidificador possui um resistor de resistência elétrica R. Sabendo que ao conectá-lo a uma tomada de 220 V ele passa a ser percorrido por uma corrente elétrica de 27,5 A, calcule a resistência elétrica desse resistor.
A) 6 Ω
B) 7 Ω
C) 8 Ω
D) 9 Ω
E) 10 Ω
Alternativa C.
Calcularemos a resistência elétrica do resistor através da sua fórmula:
\(R=\frac{U}{i}\)
\(R=\frac{220}{27,5}\)
\(R=8\ \Omega\)
Quais das alternativas apresentam a unidade de medida correspondente às grandezas físicas estudadas na eletrodinâmica?
I. A resistividade elétrica é medida em \([Ω∙m]-1\).
II. A resistência elétrica é medida em ohm.
III. A carga elétrica é medida em coulomb.
IV. A ddp elétrica é medida em volts por metro.
V. A corrente elétrica é medida em volts.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Alternativa D.
I. A resistividade elétrica é medida em \([Ω∙m]-1\). (incorreta)
A resistividade elétrica é medida em \([Ω∙m]\).
II. A resistência elétrica é medida em ohm. (correta)
III. A carga elétrica é medida em coulomb. (correta)
IV. A ddp elétrica é medida em volts por metro. (incorreta)
A ddp é medida em volts.
V. A corrente elétrica é medida em volts. (incorreta)
A corrente elétrica é medida em ampère.
